题目内容
 如图,I是△ABC的内心,且CA+AI=BC.若∠BAC=80°,则∠ABC的大小为
如图,I是△ABC的内心,且CA+AI=BC.若∠BAC=80°,则∠ABC的大小为分析:作ID⊥AC于D,IE⊥BC于E,IF⊥AB于F,由I是三角形内心,则AF+AI=BE,在线段BF上取点O,使FO=AF,△AFI≌△OFI,
从而得出IO=BO,∠FBI=∠OIB=∠IBE=
∠EAB,即可求得∠ABC和∠AIB的大小.
从而得出IO=BO,∠FBI=∠OIB=∠IBE=
| 1 |
| 2 |
解答: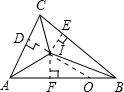 解:作ID⊥AC于D,IE⊥BC于E,IF⊥AB于F,
解:作ID⊥AC于D,IE⊥BC于E,IF⊥AB于F,
∵I是三角形内心,
∴AD=AF,CD=CE,BE=BF,AC+AI=AD+CD+AI=AF+CE+AI=BC=CE+BE,
∴AF+AI=BE,
在线段BF上取点O,使FO=AF,△AFI≌△OFI,
∴∠IAF=∠IOF AI=IO,IO+AF=IO+FO=BF
∴IO=BO,∠EBI=∠OIB=∠IBF=
∠EBA,∠ACI=∠IAF,∠IAF=∠IOF,
∵∠BAC=80°,
∴∠ABE=40°,
∴∠IBA=20°,
∵∠IAO=40°,
∴∠AIB=120°.
故答案为:40°;120°.
 解:作ID⊥AC于D,IE⊥BC于E,IF⊥AB于F,
解:作ID⊥AC于D,IE⊥BC于E,IF⊥AB于F,∵I是三角形内心,
∴AD=AF,CD=CE,BE=BF,AC+AI=AD+CD+AI=AF+CE+AI=BC=CE+BE,
∴AF+AI=BE,
在线段BF上取点O,使FO=AF,△AFI≌△OFI,
∴∠IAF=∠IOF AI=IO,IO+AF=IO+FO=BF
∴IO=BO,∠EBI=∠OIB=∠IBF=
| 1 |
| 2 |
∵∠BAC=80°,
∴∠ABE=40°,
∴∠IBA=20°,
∵∠IAO=40°,
∴∠AIB=120°.
故答案为:40°;120°.
点评:本题考查了三角形的内心,内心的性质,利用性质求得结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
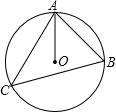 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
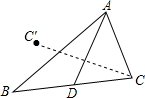 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=