题目内容
平面直角坐标系中，直线AB交x轴于点A，交y轴于点B且与反比例函数图象分别交于C、D两点，过点C作
CM⊥x轴于M，AO=6，BO=3，CM=5．求直线AB的解析式和反比例函数解析式．
解：由题意得 CM∥OB，
∴△AOB∽△AMC，
∴
即
，
∴AM=10，
∵AO=6∴MO=4，
∴点C（4，5），A（-6，0），B（0，3），
设直线解析式y1=k1x+b，
∵过点A（-6，0）和点B（0，3），
∴
b=3，
∴
，
设反比例解析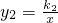
，
∵过点C（4，5），∴k2=20，
∴
．
分析：首先由过点C作CM⊥x轴于M，得 CM∥OB，所以△AOB∽△AMC，可求出AM，继而得出点A、B、C的坐标，然后设解析式，代入坐标即可求出直线AB的解析式和反比例函数解析式．
点评：此题考查的知识点是反比例函数综合应用，关键是运用相似三角形求出点的坐标，用待定系数法确定函数的解析式．
∴△AOB∽△AMC，
∴
即，∴AM=10，
∵AO=6∴MO=4，
∴点C（4，5），A（-6，0），B（0，3），
设直线解析式y1=k1x+b，
∵过点A（-6，0）和点B（0，3），
∴
b=3，∴
，设反比例解析
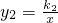，∵过点C（4，5），∴k2=20，
∴
．分析：首先由过点C作CM⊥x轴于M，得 CM∥OB，所以△AOB∽△AMC，可求出AM，继而得出点A、B、C的坐标，然后设解析式，代入坐标即可求出直线AB的解析式和反比例函数解析式．
点评：此题考查的知识点是反比例函数综合应用，关键是运用相似三角形求出点的坐标，用待定系数法确定函数的解析式．
练习册系列答案
相关题目
如图，在平面直角坐标系中，直
如图，在平面直角坐标系中，直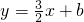
与双曲线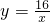
相交于第一象限内的点A，AB、AC分别垂直于x轴、y轴，垂足分别为B、C，已知四边形ABCD是正方形，求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标．
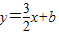与双曲线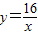
相交于第一象限内的点A，AB、AC分别垂直于x轴、y轴，垂足分别为B、C，已知四边形ABCD是正方形，求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标．