题目内容
已知:如图,以△ABC两边AB、AC为边向外作等边△ADB和△AEC,DC、BE交于点O.
(1)求证:DC=BE;
(2)求∠BOC的度数;
(3)当∠BAC度数变化时,∠BOC是否变化,说明理由.

答案:
解析:
提示:
解析:
|
(1) 证明:∵△ADB和△AEC是等边三角形,∴ AD=AB,AC=AE,∠DAB=∠CAE=60°.∴∠ DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE.在△ ADC和△ABE中,
∴△ ADC≌△ABE(SAS).∴ DC=BE.(2) 解:∵△ADC≌△ABE,∴∠ ACD=∠AEB.∵△ ACE是等边三角形,∴∠ACE=∠AEC=60°∴∠ BOC=∠OCE+∠OEC=∠ACE+∠ACD+∠OEC=∠ACE+∠AEO+∠OEC=60°+∠AEC=60°+60°=120°.( 3)解:当∠BAC度数变化时,∠BOC度数不变,仍为120°,因为在求∠BOC的度数时,未涉及到∠BAC,即∠BOC的度数与∠BAC的度数无关,所以当∠BAC变化时,∠BOC仍为120°,是定值. |
提示:
|
(1) 欲证DC=BE,只需证△ADC≌△ABE,由等边三角形的条件可得到两对对应边相等,只需证夹角∠DAC=∠BAE.(2) ∵∠BOC=∠OCE+∠OEC=∠OCA+60°+∠OEC,由(1)△DAC≌△BAE,得∠OCA=∠OEA,∴∠ BOC=∠OEA+60°+∠OEC=60°+60°=120°.( 3)由于求∠BOC时,未涉及到∠BAC,故∠BOC的大小与∠BAC无关. |

练习册系列答案
相关题目

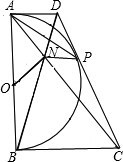 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )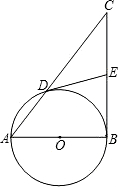 已知:如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
已知:如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.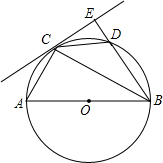 已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.
已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.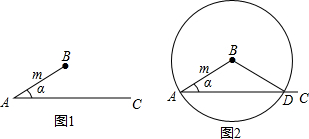

 已知:如图,以△ABC的一边BC为直径作半圆,交AB于E,过E点作半圆O的切线恰与AC垂直,试确定边BC与AC的大小关系,并证明你的结论.
已知:如图,以△ABC的一边BC为直径作半圆,交AB于E,过E点作半圆O的切线恰与AC垂直,试确定边BC与AC的大小关系,并证明你的结论.