题目内容
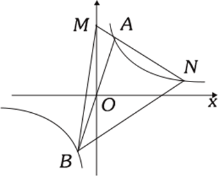
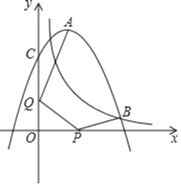
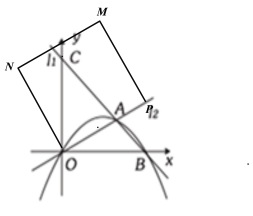
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点A,与
相交于点A,与![]() 轴相交于点B,与
轴相交于点B,与![]() 轴相交于点C,抛物线
轴相交于点C,抛物线![]() 经过点O、点A和点B,已知点A到
经过点O、点A和点B,已知点A到![]() 轴的距离等于2.
轴的距离等于2.
(1)求抛物线的解析式;
(2)点H为直线![]() 上方抛物线上一动点,当点H到
上方抛物线上一动点,当点H到![]() 的距离最大时,求点H的坐标;
的距离最大时,求点H的坐标;
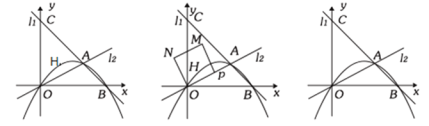
(3)如图,P为射线OA的一个动点,点P从点O出发,沿着OA方向以每秒![]() 个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
个单位长度的速度移动,以OP为边在OA的上方作正方形OPMN,设正方形POMN与△OAC重叠的面积为S,设移动时间为t秒,直接写出S与t之间的函数关系式.
【答案】(1)![]() ;(2)H;(2,2); (3)
;(2)H;(2,2); (3)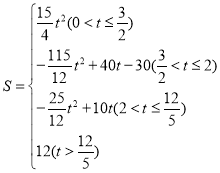 .
.
【解析】
(1)根据题意求出A、B坐标,由图像可知,图像经过原点,则c=0,设出抛物线解析式为![]() ,将A(4,2)、B(6,0)代入
,将A(4,2)、B(6,0)代入![]() ,即可得到答案.
,即可得到答案.
(2)设H(![]() ,
, ![]() ),作HD∥
),作HD∥![]() ,当HD∥
,当HD∥![]() 时,点H到
时,点H到![]() 的距离最大.设直线HD的解析式
的距离最大.设直线HD的解析式![]() ,并与抛物线解析式联立,得到一元二次方程,因为由函数图像可知,直线HD与
,并与抛物线解析式联立,得到一元二次方程,因为由函数图像可知,直线HD与![]() ,有且只有一个交点,所以△=0,求出c,进而求出H坐标,得到答案.
,有且只有一个交点,所以△=0,求出c,进而求出H坐标,得到答案.
(3)通过运动过程中,分情况讨论,并将不规则图像利用分割法求解即可.
(1)由点A到![]() 轴的距离等于2得知,A的纵坐标是2
轴的距离等于2得知,A的纵坐标是2
当y=2时,代入![]() ,得
,得![]() ,则A(4,2)
,则A(4,2)
当x=0时,代入![]() ,得y=6,则B(6,0)
,得y=6,则B(6,0)
由图像可知,图像经过原点,则c=0,则抛物线解析式为![]()
将A(4,2)、B(6,0)代入![]()
![]() 解得
解得
所以抛物线的解析式![]()
(2)

设H(![]() ,
, ![]() ),作HD∥
),作HD∥![]() ,当HD∥
,当HD∥![]() 时,点H到
时,点H到![]() 的距离最大.
的距离最大.
设直线HD的解析式![]() ,则
,则
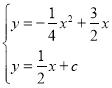 得
得![]() 化简得:
化简得:![]()
由函数图像可知,直线HD与![]() ,有且只有一个交点,所以△=
,有且只有一个交点,所以△=![]()
所以c=1
当c=1时,![]() 即为
即为![]() ,
,![]()
即![]() ,则
,则![]()
所以H(2,2)
综上所述,点H为直线![]() 上方抛物线上一动点,当点H到
上方抛物线上一动点,当点H到![]() 的距离最大时,点H的坐标H(2,2).
的距离最大时,点H的坐标H(2,2).
(3)第一种情况:下图:P点由O点运动到图(2)位置(M正好在AC上)轴时.
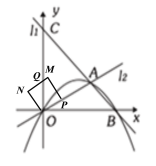
![]()
![]() ,由题意得:OP=ON=
,由题意得:OP=ON=![]() ,则MN=
,则MN=![]() .
.
![]() =
=![]() -
-![]()
=![]()
=![]()
![]()
=![]()
=![]()
作CD⊥AO,于点D,交y轴于点Q
由![]() :
:![]() ,可知B(6,0),C(0,6),则OC=6,
,可知B(6,0),C(0,6),则OC=6,
由(1)可知A(4,2),可知:![]() ,
,![]()
通过解直角三角形方法可知:![]() 即:
即:![]()
![]()
解得AD=![]() ,利用勾股定理得
,利用勾股定理得
∴![]()
∵CD⊥![]() ,MP⊥
,MP⊥![]()
∴![]() 即
即![]() 解得
解得![]()
所以![]()
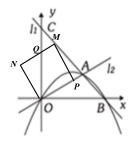
第二种情况:下图:P点图(1)位置(M正好在AC上)轴运动到O点运动到时.

![]()

取中间过程图分析面积:
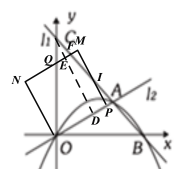
作CD⊥AO,于点D,交MN轴于点E,MN交AC于点F,MP交AC于点I.
由情况一可知![]() 则
则![]() ,代入得:
,代入得:![]()
所以,![]()
∴![]()
∵CD⊥![]() ,AP⊥
,AP⊥![]()
∴MP∥CD, ![]()
∴![]() ,则
,则![]()
∴![]()
![]() =
=![]() -
-![]() -
-![]()
=![]() -
-![]()
=![]()
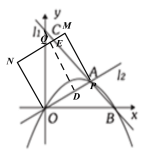
当AO=OP时,是临界点,此时![]() ,t=2
,t=2
综上所述:![]()
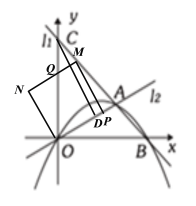
第三种情况:下图:P点图(1)位置(P与A点重合)运动到MN经过点C时.

![]()

取中间过程图分析面积:
MN交y轴于点Q,交BC于点D,由题意知:![]() ,
,![]()
![]()
=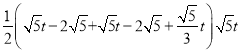
此时![]() =
=![]() -
-![]() -
-![]()
=![]() -
-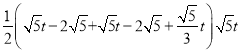
=![]()
临界点范围求值:

作CG⊥OP于点G,
OP=MP=CG=![]()
OP=![]() 即
即![]() 解得:
解得:![]()
![]()
第四种情况:下图:当△AOC完全被正方形覆盖时:
此时正方形边长>△AOC中AO边上的高,即![]() >
>![]() ,得t>
,得t>![]()
![]() =
=![]() =
=![]() A点横坐标=
A点横坐标=![]()
即当t>![]() ,S=12
,S=12
综上所述

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当4<x<1时,直接写出y的取值范围.