题目内容
(1)探究下表中的奥秘,并完成填空:| 一元二次方程 | 根 | 二次三项式 |
| x2-25=0 | x1=5,x2=-5 | x2-25=(x-5)(x+5) |
| x2+6x-16=0 | x1=2,x2=-8 | x2+6x-16=(x-2)(x+8) |
| 3x2-4x=0 | __ | 3x2-4x=3(x-__ )(x-__ ) |
| 5x2-4x-1=0 | x1=5,x2=- | 5x2-4x-1=5(x-1)(x+) |
| 2x2-3x+1=0 | __ | 2x2-3x+1=__ |
【答案】分析:(1)考查了二次三项式为0时,方程的根与二次三项式的因式分解的关系,按照题目所给规律填空即可;
(2)利用配方法解方程ax2+bx+c=0,再根据规律把ax2+bx+c因式分解.
解答:解:(1)
故本题答案为: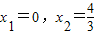 ,0,
,0, ;
;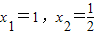 ,2(x-1)(x-
,2(x-1)(x- );
);
(2)方程ax2+bx+c=0,
移项,得ax2+bx=-c,
化系数为1,得x2+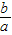 x=-
x=- ,
,
配方,得x2+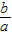 x+
x+ =-
=-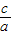 +
+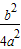 ,
,
(x+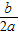 )2=
)2=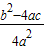 ,
,
解得,x1=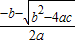 ,x2=
,x2= ,
,
∴ax2+bx+c=a(x-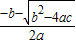 )(x-
)(x-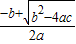 ).
).
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.
(2)利用配方法解方程ax2+bx+c=0,再根据规律把ax2+bx+c因式分解.
解答:解:(1)
| 一元二次方程 | 根 | 二次三项式 |
| x2-25=0 | x1=5,x2=-5 | x2-25=(x-5)(x+5) |
| x2+6x-16=0 | x1=2,x2=-8 | x2+6x-16=(x-2)(x+8) |
| 3x2-4x=0 | x1=0,x2= | 3x2-4x=3(x-0)(x- ) ) |
| 5x2-4x-1=0 | x1=5,x2=- | 5x2-4x-1=5(x-1)(x+) |
| 2x2-3x+1=0 | x1=1,x2= | 2x2-3x+1=2(x-1)(x- ) ) |
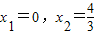 ,0,
,0, ;
;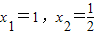 ,2(x-1)(x-
,2(x-1)(x- );
);(2)方程ax2+bx+c=0,
移项,得ax2+bx=-c,
化系数为1,得x2+
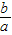 x=-
x=- ,
,配方,得x2+
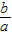 x+
x+ =-
=-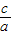 +
+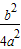 ,
,(x+
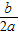 )2=
)2=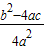 ,
,解得,x1=
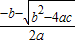 ,x2=
,x2= ,
,∴ax2+bx+c=a(x-
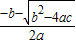 )(x-
)(x-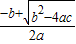 ).
).点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
探究下表中的奥秘,并完成填空:
将你发现的结论一般化,并写出来.
| 一元二次方程 | 两个根 | 二次三项式因式分解 | ||||
| x2-2x+1=0 | x1=1,x2=1 | x2-2x+1=(x-1)(x-1) | ||||
| x2-3x+2=0 | x1=1,x2=2 | x2-3x+2=(x-1)(x-2) | ||||
| 3x2+x-2=0 | x1=
|
3x2+x-2=3(x-
| ||||
| 2x2+5x+2=0 | x1=-
|
2x2+5x+2=2(x+
| ||||
| 4x2+13x+3=0 | x1= |
4x2+13x+3=4(x+ |
探究下表中的奥秘,并完成填空.
对于一般的二次三项式ax2+bx+c,用你发现的结论对ax2+bx+c进行因式分解.
| 一元二次方程 | 两个根 | 二次三项式因式分解 | ||||
| x2-2x+1=0 | x1=1,x2=1 | x2-2x+1=(x-1)(x-1) | ||||
| x2-3x+2=0 | x1=1,x2=2 | x2-3x+2=(x-1)(x-2) | ||||
| 3x2+x-2=0 | x1=
|
3x2+x-2=3(x-
| ||||
| 2x2+5x+2=0 | x1=-
|
2x2+5x+2=2(x+
| ||||
| 4x2+13x+3=0 | x1= |
4x2+13x+3=4(x+ |
(1)探究下表中的奥秘,并完成填空:
(2)仿照上表把二次三项式ax2+bx+c(其中b2-4ac≥0)进行分解?
| 一元二次方程 | 根 | 二次三项式 |
| x2-25=0 | x1=5,x2=-5 | x2-25=(x-5)(x+5) |
| x2+6x-16=0 | x1=2,x2=-8 | x2+6x-16=(x-2)(x+8) |
| 3x2-4x=0 | __ | 3x2-4x=3(x-__ )(x-__ ) |
| 5x2-4x-1=0 | x1=5,x2=- | 5x2-4x-1=5(x-1)(x+) |
| 2x2-3x+1=0 | __ | 2x2-3x+1=__ |
