Question

【题目】综合与探究：

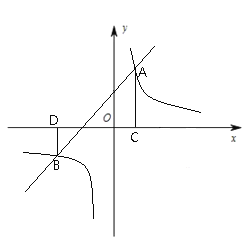
如图所示，在平面直角坐标系中，直线与反比例函数的图象交于，两点，过点作轴于点，过点作轴于点．

（1）求，的值及反比例函数的函数表达式；

（2）若点在线段上，且，请求出此时点的坐标；

（3）小颖在探索中发现：在轴正半轴上存在点，使得是以为顶角的等腰三角形.请你直接写出点的坐标.

Answer 1

【答案】（1），，；（2）点的坐标为；（3）

【解析】

（1）利用点在直线上，将点的坐标代入直线解析式中求解即可求出a，b，最后用待定系数法求出反比例函数解析式；

（2）设点，用三角形的面积公式得到求解即可得出结论；

（3）设出点M坐标，表示出MA2=（m-1）2+9，AB2=32，根据等腰三角形的性质建立方程求解即可得出结论．

解：（1）∵直线与反比例函数的图象交与，两点

∴，.

∴，.

∴，.

∵点在反比例函数上，

∴.

∴反比例函数的函数表达式为.

（2）设点，

∵，∴.

∴.

∵，∴.

∴，

∵

∴.

解得：，

∴.

∴点的坐标为.

（3）设出点M坐标为（m,0），

∴MA2=（m-1）2+9，AB2=（1+3）2+（3+1）2=32，

∵是以为顶角的等腰三角形

∴AM=AB,

故（m-1）2+9=32

解得m=或m=（舍去）

∴