题目内容
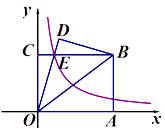
【题目】如图，△ABC是等腰直角三角形，∠C=90°，点D是AB的中点，点E，F分别在BC，AC上，且AF=CE．
（1）填空：∠A的度数是 ．
（2）探究DE与DF的关系，并给出证明．
【答案】（1）45°；（2）DE=DF，DE⊥DF
【解析】分析：（1）根据
是等腰直角三角形定义可得：
（2）连接CD，首先根据是等腰直角三角形，
，点D是AB的中点得到
从而得到
≌
，证得
详解：(1)∵△ABC是等腰直角三角形,
∴
故答案为：
；
(2)DE=DF，DE⊥DF，
证明：连接CD，
∵△ABC是等腰直角三角形,∠C=
，点D是AB的中点，
∴CD=AD=BD，CD⊥AD，
∴
∵AF=CE，
∴△DCE≌△DAF(SAS)，
∴DE=DF，∠ADF=∠CDE，
∴∠ADF+∠FDC=∠CDE+∠FDC，
∵∠CDA=，
∴∠EDF=，
∴DE=DF，DE⊥DF.
练习册系列答案
相关题目
【题目】我市某中学举行“中国梦校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图4所示．
（1）根据图示填写下表：
平均数（分） | 中位数（分） | 众数（分） | |
初中部 | 85 | ||
高中部 | 85 | 100 |
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
