Question

【题目】如图，以G（0，2）为圆心，半径为4的圆与x轴交于A，B两点，与y轴交于C，D两点，点E为⊙G上一动点，且点E在第一象限，CF⊥AE于点F，当点E在⊙G的圆周上运动的过程中，线段BF的长度的最小值为（　　）

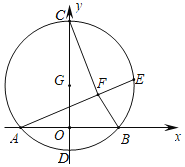
A.3B.22C.6﹣2D.4

Answer 1

【答案】C

【解析】

要求线段BF的最小值，首先要找到点F的运动轨迹，根据分析计算可知点F的运动轨迹是以AC为直径的圆，求出圆心与点B之间的距离，然后用该距离减去半径就是线段BF的最小值.

连接AC、BC，如图所示：

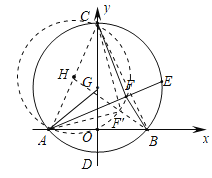
∵以G（0，2）为圆心，半径为4的圆与x轴交于A，B两点，与y轴交于C，D两点，

∴OC＝6，OG＝2，AG＝4，OA＝OB，AC＝BC，

∴OA2，

AB＝2OA＝2×24，

∵CF⊥AE，

∴∠CFA＝90°，

在中，由勾股定理得

AC4，

∴点F的运动轨迹是以AC为直径的圆，设圆心为H，连接BH交⊙H于点F′，则BF′即为线段BF的最小长度，

∵AC＝BC＝AB＝4，

∴△ABC是等边三角形，

∴△ABH是直角三角形，

AHAC42，

BH6，

∴BF′＝BH﹣HF′＝BH﹣AH＝6﹣2，

故选：C．