题目内容
实数x,y,z,w满足| (22x+1)(22y+2)(22z+4)(22w+8) | 128 |
分析:首先将原等式进行化简,然后根据等式左右两边质因数分解的具体情况判断出四个未知数的值.
解答:解:原式可化为
=2x+y+z+w;
即(22x+1)(22y-1+1)(22z-2+1)(22w-3+1)=2x+y+z+w+1;
等式的右边是2的幂乘积的形式,那么根据质因数分解定理知:等式左边也必须是2的幂相乘的形式;
显然,22x=22y-1=22z-2=22w-3=1,即2x=2y-1=2x-2=2w-3=0,
解得:x=0,y=
,z=1,w=
,
所以x2+y2+z2+w2=
.
| (22x+1)(22y-1+1)(22z-2+1)(22w-3+1)• 21+2+3 |
| 27 |
即(22x+1)(22y-1+1)(22z-2+1)(22w-3+1)=2x+y+z+w+1;
等式的右边是2的幂乘积的形式,那么根据质因数分解定理知:等式左边也必须是2的幂相乘的形式;
显然,22x=22y-1=22z-2=22w-3=1,即2x=2y-1=2x-2=2w-3=0,
解得:x=0,y=
| 1 |
| 2 |
| 3 |
| 2 |
所以x2+y2+z2+w2=
| 7 |
| 2 |
点评:题目中既用到了分式的基本性质、幂的运算,还涉及到质因数分解的相关知识,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
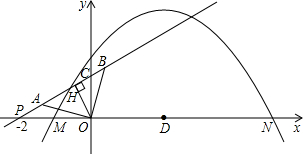 E点,直线NE与直线AB的交点G是否总满足PB•PG<10
E点,直线NE与直线AB的交点G是否总满足PB•PG<10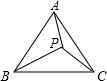 如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.
如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积. (2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式
(2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式