Question

【题目】提出问题：

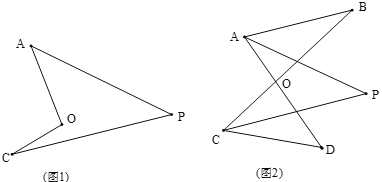
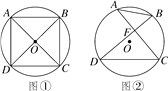
（1）如图，我们将图（1）所示的凹四边形称为“镖形”．在“镖形”图中，∠AOC与∠A、∠C、∠P的数量关系为_______.

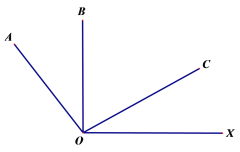
（2）如图（2），已知AP平分∠BAD，CP平分∠BCD，∠B =28°，∠D=48°．求∠P的度数．

由（1）结论得：∠AOC =∠PAO +∠PCO+∠P

所以2∠AOC=2∠PAO +2∠PCO+2∠P即2∠AOC =∠BAO +∠DCO+2∠P

因为∠AOC =∠BAO +∠B，∠AOC =∠DCO +∠D

所以2∠AOC=∠BAO +∠DCO+∠B +∠D

所以∠P=_______.

解决问题：

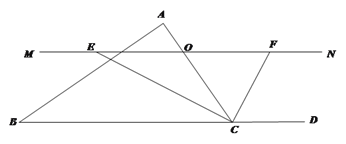
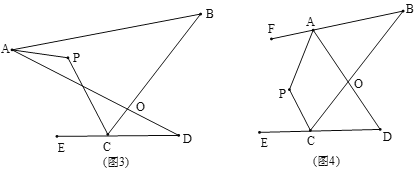
（3）如图（3），直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是_______；

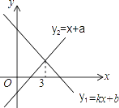
（4）如图（4），直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是_______.

Answer 1

【答案】（1）∠AOC=∠A+∠P+∠C；（2）38°；（3）∠P=90°+（∠B+∠D）；（4）∠P=180°-（∠B+∠D）.

【解析】

（1）延长CO，交AP与B，根据三角形外角性质即可得答案；（2）根据2∠AOC=∠BAO +∠DCO+2∠P，2∠AOC=∠BAO +∠DCO+∠B+∠D，可得2∠P=∠B+∠D，进而可得答案；（3）由角平分线的定义可得∠PAB=∠PAD，∠PCB=∠PCE，根可三角形内角和定理可得2∠PAB+∠B=180°-2∠PCB+∠D，由（1）可知∠P=∠PAB+∠B+∠PCB，利用等量代换即可得答案；（4）由角平分线的定义可得∠FAP=∠PAD，∠PCE=∠PCB，根据四边形的内角和等于360°可得（180°-∠FAP）+∠P+∠PCB+∠B=360°，∠PAD+∠P+（180°-∠PCE）+∠D=360°，然后整理即可得解；

（1）如图，延长CO，交AP与B，

∵∠AOC=∠A+∠ABO，∠ABO=∠C+∠P，

∴∠AOC=∠A+∠P+∠C，

故答案为：∠AOC=∠A+∠P+∠C，

（2）∵2∠AOC =∠BAO +∠DCO+2∠P，2∠AOC=∠BAO +∠DCO+∠B+∠D，

∴2∠P=∠B+∠D，

∴∠P=（28°+48°）=38°，

故答案为：38°

（3）∵直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，

∴∠PAB=∠PAD，∠PCB=∠PCE，

∴2∠PAB+∠B=180°-2∠PCB+∠D，

∴180°-2（∠PAB+∠PCB）+∠D=∠B

∵∠P=∠PAB+∠B+∠PCB，

∴∠PAB+∠PCB=∠P-∠B，

∴180°-2（∠P-∠B）+∠D=∠B，即∠P=90°+（∠B+∠D）.

（4）∵直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，

∴∠FAP=∠PAO，∠PCE=∠PCB，

在四边形APCB中，（180°-∠FAP）+∠P+∠PCB+∠B=360°①，

在四边形APCD中，∠PAD+∠P+（180°-∠PCE）+∠D=360°②，

①+②得：2∠P+∠B+∠D=360°，

∴∠P=180°-（∠B+∠D）.