题目内容
14．海滩上有一堆桃子，第一天猴子吃掉这堆桃子的$\frac{2}{5}$，又将4个扔到大海中，第二天猴子吃掉的桃子数加上3个就是第一天所剩桃子数的$\frac{5}{8}$，若第二天剩下6个桃子，问海滩上原有多少个桃子？分析 设海滩上原有x个桃子，由题意得第一天吃掉桃子数为：$\frac{2}{5}$x，还剩桃子数：（1-$\frac{2}{5}$）x-4=$\frac{3}{5}$x-4；第二天吃掉的桃子数为：$\frac{5}{8}$[（1-$\frac{2}{5}$）x-4]-3=$\frac{3}{8}$x-$\frac{11}{2}$，根据第二天剩下6个桃列出方程，再解即可．
解答 解：设海滩上原有x个桃子，由题意得：
第一天吃掉桃子数为：$\frac{2}{5}$x，
第一天还剩桃子数：（1-$\frac{2}{5}$）x-4=$\frac{3}{5}$x-4；
第二天吃掉的桃子数为：$\frac{5}{8}$[（1-$\frac{2}{5}$）x-4]-3=$\frac{3}{8}$x-$\frac{11}{2}$，
由题意得：x-（$\frac{2}{5}$x+4）-（$\frac{3}{8}$x-$\frac{11}{2}$）=6，
解得：x=20．
答：海滩上原有20个桃子．
点评 此题主要考查了一元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．
练习册系列答案
相关题目
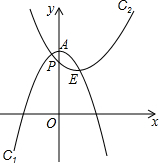如图，点A、点E的坐标分别为 （0，3）与（1，2），以点A为顶点的抛物线记为C1：y1=-x2+n；以E为顶点的抛物线记为C2：y2=ax2+bx+c，且抛物线C2与y轴交于点P（0，$\frac{5}{2}$）．
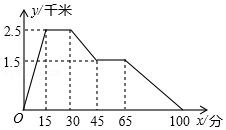如图反映的是小华从家里跑步去体育馆，在那里锻炼了一阵后又走到文具店去买笔，然后走回家，其中x表示时间，y表示小华离家的距离．根据图象回答下列问题：