题目内容
已知:抛物线y=(k-1)x2+2kx+k-2与x轴有两个不同的交点.

(1)求k的取值范围;
(2)当k为整数,且关于x的方程3x=kx-1的解是负数时,求抛物线的解析式;
(3)在(2)的条件下,若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形,使得正方形的一边在x轴上,其对边的两个端点在抛物线上,试求出这个最大正方形的边长.
答案:
解析:
解析:
|
解:(1) 依题意,得 ∴ (2)解方程 ∵方程 ∴ 综合①②,及 ∴抛物线解析式为 (3)如图,设最大正方形ABCD的边长为m,则B、C两点的纵坐标为 且由对称性可知:B、C两点关于抛物线对称轴对称. ∵抛物线的对称轴为: ∴点C的坐标为 ∵C点在抛物线上, ∴ 整理,得 ∴ ∴
|

练习册系列答案
相关题目

 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).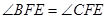 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由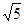 个单位长度、每秒2
个单位长度、每秒2
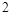 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).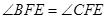 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由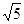 个单位长度、每秒2
个单位长度、每秒2