题目内容
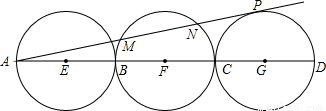
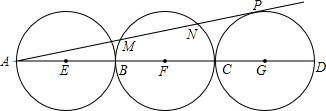如图，已知AD=30，点B，C是AD上的三等分点，分别以AB，BC，CD为直径作圆，圆心分别为E，F，G，AP切⊙G于点P，交⊙F于M，N，求弦MN的长．分析：连接PG、MF，过F作FQ⊥MN于点Q，易证△AFQ∽△AGP，根据相似三角形的性质即可求得QF的长，然后利用垂径定理即可求解．
解答：解：连接PG、MF，过F作FQ⊥MN于点Q．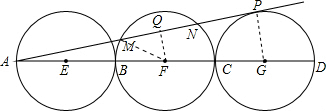
∵AD=30，点B，C是AD上的三等分点，
∴AE=BE=BF=CF=CG=DG=5，
则AG=25，PG=5，
∵AD是圆的切线，
∴PG⊥AD，
又∵FQ⊥MN，
∴△AFQ∽△AGP，
∴
=
=
，
∴FQ=
PG=3，
在直角△FQM中，MQ=
=
=4，
则MN=2MQ=8．
∵AD=30，点B，C是AD上的三等分点，
∴AE=BE=BF=CF=CG=DG=5，
则AG=25，PG=5，
∵AD是圆的切线，
∴PG⊥AD，
又∵FQ⊥MN，
∴△AFQ∽△AGP，
∴
| FQ |
| PG |
| AF |
| AG |
| 3 |
| 5 |
∴FQ=
| 3 |
| 5 |
在直角△FQM中，MQ=
| MF2-FQ2 |
| 52-32 |
则MN=2MQ=8．
点评：本题是垂径定理，切线的性质定理以及相似三角形的判定与性质的综合应用，正确作出辅助线是关键．
练习册系列答案
名校课堂系列答案
相关题目
