Question

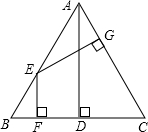如图，AD是等边三角形ABC的高，点E在AB上，EF⊥BC于F，EG⊥AC于G．请判断EF+EG与AD的大小，并说明理由．

Answer 1

分析：等边三角形的三边相等，连接EC，可用面积相等证得结果．

解答：解：EF+EG=AD．
连接EC，则S△ABC=S△EBC+S△ECA=

1

2

BC•EF+

1

2

AC•EG．
∵BC=AC，
∴S△ABC=

1

2

BC(EF+EG)．
又∵S△ABC=

1

2

BC•AD．
∴EF+EG=AD．

点评：本题考查等边三角形的性质，关键是作出辅助线，利用面积相等求解．