题目内容
 如图,已知直线y=
如图,已知直线y= x与双曲线y=
x与双曲线y= (k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y= (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为________.
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为________.
(2,4)或(8,1)
分析:把点B的坐标代入反比例函数解析式求出k值,再根据反比例函数图象的中心对称性求出点A的坐标,然后过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,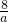 ),然后根据S△AOC=S△COF+S梯形ACFE-S△AOE列出方程求解即可得到a的值,从而得解.
),然后根据S△AOC=S△COF+S梯形ACFE-S△AOE列出方程求解即可得到a的值,从而得解.
解答: 解:∵点B(-4,-2)在双曲线y=
解:∵点B(-4,-2)在双曲线y= 上,
上,
∴ =-2,
=-2,
∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,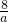 ),
),
若S△AOC=S△COF+S梯形ACFE-S△AOE,
= ×8+
×8+ ×(2+
×(2+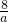 )(4-a)-
)(4-a)- ×8,
×8,
=4+ -4,
-4,
= ,
,
∵△AOC的面积为6,
∴ =6,
=6,
 整理得,a2+6a-16=0,
整理得,a2+6a-16=0,
解得a1=2,a2=-8(舍去),
∴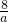 =
= =4,
=4,
∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE-S△COF= ,
,
∴ =6,
=6,
解得:a=8或a=-2(舍去)
∴点C的坐标为(8,1).
故答案为:(2,4)或(8,1).
点评:本题考查了反比例函数与一次函数的交点问题,反比例函数系数的几何意义,作辅助线并表示出△ABC的面积是解题的关键.
分析:把点B的坐标代入反比例函数解析式求出k值,再根据反比例函数图象的中心对称性求出点A的坐标,然后过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,
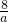 ),然后根据S△AOC=S△COF+S梯形ACFE-S△AOE列出方程求解即可得到a的值,从而得解.
),然后根据S△AOC=S△COF+S梯形ACFE-S△AOE列出方程求解即可得到a的值,从而得解.解答:
 解:∵点B(-4,-2)在双曲线y=
解:∵点B(-4,-2)在双曲线y= 上,
上,∴
 =-2,
=-2,∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,
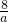 ),
),若S△AOC=S△COF+S梯形ACFE-S△AOE,
=
 ×8+
×8+ ×(2+
×(2+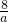 )(4-a)-
)(4-a)- ×8,
×8,=4+
 -4,
-4,=
 ,
,∵△AOC的面积为6,
∴
 =6,
=6, 整理得,a2+6a-16=0,
整理得,a2+6a-16=0,解得a1=2,a2=-8(舍去),
∴
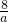 =
= =4,
=4,∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE-S△COF=
 ,
,∴
 =6,
=6,解得:a=8或a=-2(舍去)
∴点C的坐标为(8,1).
故答案为:(2,4)或(8,1).
点评:本题考查了反比例函数与一次函数的交点问题,反比例函数系数的几何意义,作辅助线并表示出△ABC的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )