题目内容
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.

(1)证明:∵AC为直径,
∴∠ADC=90°,
∴∠A+∠DCA=90°,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
解:连接DO,
∵DO=CO,
∴∠1=∠2,
∵DM=CM,
∴∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴直线DM与⊙O相切.


 考前必练系列答案
考前必练系列答案为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
| 居民(户) | 1 | 3 | 2 | 4 |
| 月用电量(度/户) | 40 | 50 | 55 | 60 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
|
| A. | 中位数是55 | B. | 众数是60 | C. | 方差是29 | D. | 平均数是54 |
第六次全国人口普查数据显示,德州市常驻人口约为556.82万人,此数用科学记数法表示正确的是( )
|
| A. | 556.82×104 | B. | 5.5682×102 | C. | 5.5682×106 | D. | 5.5682×105 |
分式方程 ﹣1=
﹣1= 的解是( )
的解是( )
|
| A. | x=1 | B. | x=﹣1+ | C. | x=2 | D. | 无解 |
某学生用品商店,计划购进A、B两种背包共80件进行销售,购货资金不少于2090元,但不超过2096元,两种背包的成本和售价如下表:
| 种 类 | 成本(元/件) | 售价(元/件) |
| A | 25 | 30 |
| B | 28 | 35 |
假设所购两种背包可全部售出,请回答下列问题:
⑴ 该商店对这两种背包有哪几种进货方案?
⑵ 该商店如何进货获得利润最大?
⑶ 根据市场调查,每件B种背包的市价不会改变,每件A种背包的售价将会提高 元(
元(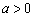 ),该商店又将如何进货获得的利润最大?
),该商店又将如何进货获得的利润最大?



 )﹣2﹣|﹣
)﹣2﹣|﹣ ﹣2|+(
﹣2|+( ﹣1.414)0﹣3tan30°﹣
﹣1.414)0﹣3tan30°﹣ .
.
