题目内容
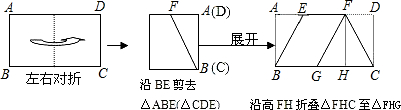
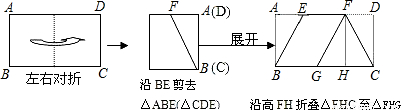
 如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为( )
如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为( )分析:先根据翻折变换的性质得出∠1=∠D′MN,∠2=∠D′NM,再由平行线的性质求出∠1+∠=∠D′MN及∠2+∠D′NM的度数,进而可得出结论.
解答: 解:∵△MND′由△MND翻折而成,
解:∵△MND′由△MND翻折而成,
∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN=
=
=25°,∠2=∠D′NM=
=
=75°,
∴∠D=180°-∠1-∠2=180°-25°-75°=80°.
故选C.
 解:∵△MND′由△MND翻折而成,
解:∵△MND′由△MND翻折而成,∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN=
| ∠A |
| 2 |
| 50° |
| 2 |
| ∠C |
| 2 |
| 150° |
| 2 |
∴∠D=180°-∠1-∠2=180°-25°-75°=80°.
故选C.
点评:本题考查的是翻折变换的性质及平行线的性质,解答此类题目时往往隐含了三角形的内角和是180°这一知识点.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目