题目内容
在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC=________.
6
分析:根据题意做出图形,过点A作AD⊥BC于D,根据AB=AC=5,sin∠ABC=0.8,可求出AD的长度,然后根据勾股定理求出BD的长度,继而可求出BC的长度.
解答: 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD,
在Rt△ABD中,
∵sin∠ABC= =0.8,
=0.8,
∴AD=5×0.8=4,
则BD=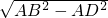 =3,
=3,
∴BC=BD+CD=3+3=6.
故答案为:6.
点评:本题考查了解直角三角形的知识,难度一般,解答本题的关键是构造直角三角形并解直角三角形以及勾股定理的应用.
分析:根据题意做出图形,过点A作AD⊥BC于D,根据AB=AC=5,sin∠ABC=0.8,可求出AD的长度,然后根据勾股定理求出BD的长度,继而可求出BC的长度.
解答:
 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,∵AB=AC,
∴BD=CD,
在Rt△ABD中,
∵sin∠ABC=
 =0.8,
=0.8,∴AD=5×0.8=4,
则BD=
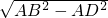 =3,
=3,∴BC=BD+CD=3+3=6.
故答案为:6.
点评:本题考查了解直角三角形的知识,难度一般,解答本题的关键是构造直角三角形并解直角三角形以及勾股定理的应用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 (2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE=
(2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE= (2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.
(2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N. 如图,在△ABC中,AB=AC,把△ABC绕着点A旋转至△AB1C1的位置,AB1交BC于点D,B1C1交AC于点E.求证:AD=AE.
如图,在△ABC中,AB=AC,把△ABC绕着点A旋转至△AB1C1的位置,AB1交BC于点D,B1C1交AC于点E.求证:AD=AE. (2013•滨湖区一模)如图,在△ABC中,AB是⊙O的直径,∠B=60°,∠C=70°,则∠BOD的度数是( )
(2013•滨湖区一模)如图,在△ABC中,AB是⊙O的直径,∠B=60°,∠C=70°,则∠BOD的度数是( ) (2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.