题目内容
(1)如图1,△ABC的面积是10,E是BC的中点,连接AE,△AEC的面积是______;
(2)如图2,四边形ABCD的面积是10,E、F分别是一组对边AB、CD的中点,连接AF,CE,则四边形AECF的面积是______;
(3)如图3,E、F分别是一组对边AB、CD上的点,且AE= AB,CF=
AB,CF= CD,若四边形ABCD的面积是10,连接AF,CE,则四边形AECF的面积是______;
CD,若四边形ABCD的面积是10,连接AF,CE,则四边形AECF的面积是______;
(4)如图4,平行四边形ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒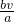 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请求出这个值;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请求出这个值;若变化,说明是怎样变化的.

 解:(1)△AEC和△ABC,高相同,底边相差一半,
解:(1)△AEC和△ABC,高相同,底边相差一半,又∵△ABC的面积是10
∴△AEC的面积是5.
(2)由图形可得△AEC是△ABC面积的一半,△AFC是△ADC面积的一半,
∴四边形AECF的面积=
 四边形ABCD的面积=5.
四边形ABCD的面积=5.(3)由图形可得△AEC是△ABC面积的
 ,△AFC是△ADC面积的
,△AFC是△ADC面积的 ,
,∴四边形AECF的面积=
 四边形ABCD的面积=
四边形ABCD的面积= .
.(4)四边形DEBF的面积的值不随时间t的变化而变化;
∵AE=vt,AB=a,
∴
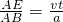 ,
,∵BF=
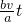 ,BC=b,
,BC=b,∴
 ,
,∵△AED与△ABD同底,
∴
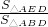 =
= ,
,∵△DBF与△DBC同底,
∴
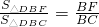 ,
,∴
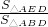 =
= ,
,∵S△ABD=S△DBC,
∴S△AED=S△DBF,
∴
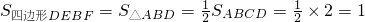 .
.分析:(1)根据△AEC和△ABC,高相同,底边相差一半可得出答案.
(2)(3)连接AC,在△ACD和△ACB中,根据底边与高的关系可得出四边形AECF与四边形ABCD的面积的关系.、
(4)根据同底等高的三角形的面积相等,结合(1)(2)(3)的结论即可做出解答.
点评:本题考查了平行四边形的性质及三角形的面积,属于综合题,解答本题关键是要掌握高相同,底边在一条直线上的三角形的面积比等于底边之比.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,如果AB∥CD,那么下面说法错误的是( )
如图,如果AB∥CD,那么下面说法错误的是( ) 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF. 如图,直线AB、CD被直线CE所截.
如图,直线AB、CD被直线CE所截.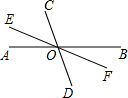 如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( )
如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( ) 如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.
如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.