Question

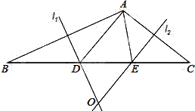
【题目】如图，△A1B1C1是边长为1的等边三角形，A2为等边△A1B1C1的中心，连接A2B1并延长到点B2 ， 使A2B1=B1B2 ， 以A2B2为边作等边△A2B2C2 ， A3为等边△A2B2C2的中心，连接A3B2并延长到点B3 ， 使A3B2=B2B3 ， 以A3B3为边作等边△A3B3C3 ， 依次作下去得到等边△AnBnCn ， 则等边△A6B6C6的边长为 ．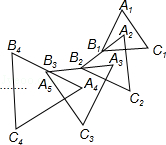

Answer 1

【答案】
【解析】解：作A2D1⊥A1B1于D1 ， A3D2⊥A2B2于D2 ， 如图， ∵△A1B1C1是边长为1的等边三角形，A2为等边△A1B1C1的中心，
∴∠A2B1D1=30°，B1D1= A1B1= ，
∴cos∠A2B1D1=cos30°= = ，
∴A2B1= ，
∵A2B1=B1B2 ，
∴A2B2= ，
同理可得∠A3B2D2=30°，B2D2= A2B2= × = ，
∴cos∠A3B2D2=cos30°= = ，
∴A3B2= ，
∵A3B2=B2B3 ，
∴A3B3= =（ ）2 ，
同理可得A4B4=（ ）3 ，
A5B5=（ ）4 ． A6B6C=（ ）5= ，
故答案为 ．

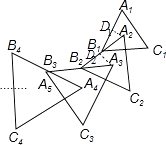
作A2D1⊥A1B1于D1 ， A3D2⊥A2B2于D2 ， 根据等边三角形的中心的性质得∠A2B1D1=30°，B1D1= A1B1= ，利用余弦的定义得cos∠A2B1D1=cos30°= = ，可计算出A2B1= ，由A2B1=B1B2得到A2B2= ，用同样的方法可计算出A3B3=（ ）2 ， 特殊的结论．