题目内容
8.若关于x,y的二元一次方程组$\left\{\begin{array}{l}3x-y=1+t\\ x+3y=3\end{array}\right.$的解满足2x+y≤2,则t的取值范围为t≤0.分析 先把先把两式相加求出4x+2y的值,再代入2x+y≤2中得到关于t的不等式,求出的取值范围即可.
解答 解:$\left\{\begin{array}{l}{3x-y=1+t①}\\{x+3y=3②}\end{array}\right.$,
①+②得,4x+2y=4+t,
∵2x+y≤2,
∴4x+2y≤4,
可得:4+t≤4,
解得:t≤0,
故答案为:t≤0.
点评 本题考查的是解二元一次方程组及解二元一次不等式组,解答此题的关键是把t当作已知条件表示出x、y的值,再得到关于t的不等式.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.实数-2的绝对值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -2 |
3.我国古代问题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长、井深各几何?(注:绳儿折即把绳平均分成几等分.)( )
| A. | 36,8 | B. | 28,6 | C. | 28,8 | D. | 13,3 |
6.“大嘴猴”童装店最近销售了某种夏装30件,销售量如下表所示:则所销售夏装尺码的中位数是( )
| 尺码(厘米) | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 销售量(件) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
| A. | 105 | B. | 110 | C. | 115 | D. | 120 |
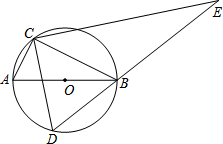 如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.
如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.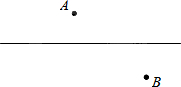 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?