题目内容
27、如图1,两个不全等的四边形ABCD、四边形CGFE是正方形,连接BG,DE.交DC于H,交CG于K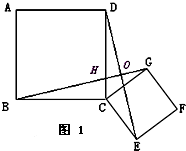
(1)观察图形,①猜想BG与DE之间长度关系;②猜想BG与DE所在直线的位置关系,并证明你的猜想.
直接回答:连接四边形DBEG四边中点所得四边形是
(2)如图2,将原题中正方形改为菱形,且∠BCD=∠GCE=90°.则(1)中的①、②的结论是否成立?若成立,请证明;若不成立,请说明理由.
直接回答:连接四边形DBEG四边中点所得四边形是
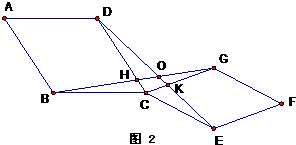
(3)如图3,将原题中正方形改为矩形,且BC=mCG、CD=mCE则(1)中的①、②结论是否成立?不要证明
直接回答:连接四边形DBEG四边中点所得四边形是


(1)观察图形,①猜想BG与DE之间长度关系;②猜想BG与DE所在直线的位置关系,并证明你的猜想.
直接回答:连接四边形DBEG四边中点所得四边形是
正方
形(2)如图2,将原题中正方形改为菱形,且∠BCD=∠GCE=90°.则(1)中的①、②的结论是否成立?若成立,请证明;若不成立,请说明理由.
直接回答:连接四边形DBEG四边中点所得四边形是
正方
形
(3)如图3,将原题中正方形改为矩形,且BC=mCG、CD=mCE则(1)中的①、②结论是否成立?不要证明
直接回答:连接四边形DBEG四边中点所得四边形是
矩
形.
分析:(1)根据正方形的性质得到BC=DC,CE=CG,∠BCD=∠GCE=90°,推出∠BCG=∠ECD,根据SAS证△BCG≌△DCE,得到BG=DE,∠GBC=∠CDE,根据三角形的内角和定理求出∠DOH即可;
(2)根据正方形的判定证出是正方形,由(1)说明即可;
(3)根据三角形的中位线定理证出是平行四边形,根据对角线垂直证出一个角是直角,即可得出答案.
(2)根据正方形的判定证出是正方形,由(1)说明即可;
(3)根据三角形的中位线定理证出是平行四边形,根据对角线垂直证出一个角是直角,即可得出答案.
解答:(1)解:①BG与DE之间长度关系是BG=DE,②BG与DE所在直线的位置关系是BG⊥DE,
证明:∵正方形ABCD、EFGC,
∴BC=DC,CE=CG,∠BCD=∠GCE=90°,
∴∠BCG=∠ECD,
∴△BCG≌△DCE,
∴BG=DE,∠GBC=∠CDE,
∵∠GBC+∠BHC=90°,
∴∠CDE+∠DEG=90°,
∴∠DOH=180°-90°=90°,
∴BG⊥DE.
故答案为:正方.
(2)成立,
证明:∵菱形ABCD、EFGC,
∵∠BCD=∠GCE=90°,
∴菱形ABCD、EFGC是正方形,
由(1)证出BG=DE,BG⊥DE,
∴仍成立.
故答案为:正方.
(3)答:①不成立,②成立,
故答案:矩.
证明:∵正方形ABCD、EFGC,
∴BC=DC,CE=CG,∠BCD=∠GCE=90°,
∴∠BCG=∠ECD,
∴△BCG≌△DCE,
∴BG=DE,∠GBC=∠CDE,
∵∠GBC+∠BHC=90°,
∴∠CDE+∠DEG=90°,
∴∠DOH=180°-90°=90°,
∴BG⊥DE.
故答案为:正方.
(2)成立,
证明:∵菱形ABCD、EFGC,
∵∠BCD=∠GCE=90°,
∴菱形ABCD、EFGC是正方形,
由(1)证出BG=DE,BG⊥DE,
∴仍成立.
故答案为:正方.
(3)答:①不成立,②成立,
故答案:矩.
点评:本题主要考查对三角形的中位线定理,正方形的性质和判定,矩形的性质和判定,平行四边形的判定,全等三角形的性质和判定,三角形的内角和定理,垂直的定义,菱形的性质等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目

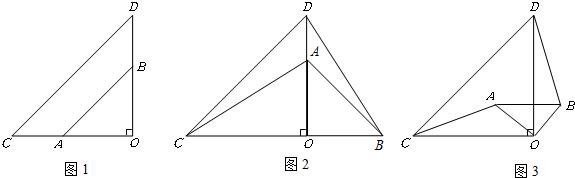

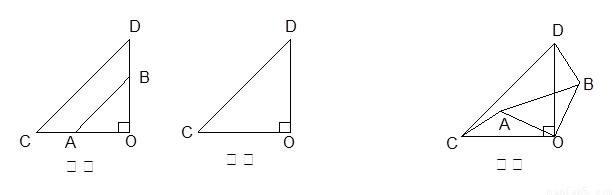
 绕点O顺时针旋转
绕点O顺时针旋转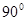 ,在图乙中作出旋转后的
,在图乙中作出旋转后的