Question

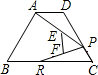（2012•海淀区二模）如图，在梯形ABCD中，AD∥BC，∠ABC=60°，AB=DC=2，AD=1，R、P分别是BC、CD边上的动点（点R、B不重合，点P、C不重合），E、F分别是AP、RP 的中点，设BR=x，EF=y，则下列图象中，能表示y与x的函数关系的图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：先根据余弦定理得出AR²=AB²+BR²-2cosB•AB•BR=4+x²-2x，再根据E、F分别是AP、RP 的中点，得出EF=

1

2

AR，从而得出4y²=x²-2x+4（y＞0），即可得出y与x的函数关系的大致图象．

解答：解：过点A作AG⊥BC，垂足为G，
∵∠ABC=60°，AB=2，
∴AG=sin∠ABC•AB=

3

2

×2=

3

，
BG=cos∠ABC•AB=

1

2

×2=1，
∵BR=x，
∴GR=

.

x-1

.

，
∴AR²=AG²+GR²
=（

3

）²+（1-x）²
=4+x²-2x，
∵E、F分别是AP、RP 的中点，
∴EF=

1

2

AR，
∴EF²=

1

4

AR²，
∴y²=

1

4

（4+x²-2x）
∵y＞0，
∴y=

1

2

x2-2x+4

，
∵当x=3时，y=

7

2

，
∴从图象可知A、B、D不符合题意，C符合，
故选C．

点评：此题考查了动点问题的函数图象，解题的关键是根据余弦定理和中位线定理得出y与x的函数关系，是一道综合题．