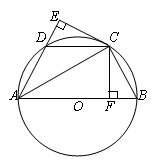
题目内容
已知 是半圆
是半圆 的直径, 点
的直径, 点 在
在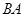 的延长线上运动(点
的延长线上运动(点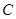 与点
与点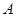 不重合), 以
不重合), 以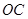 为直径的半圆
为直径的半圆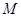 与半圆
与半圆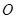 交于点
交于点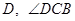 的平分线与半圆
的平分线与半圆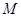 交于点
交于点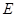 .
.
如图甲, 求证: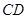 是半圆
是半圆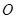 的切线;
的切线;
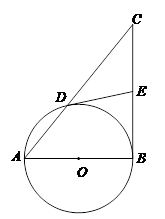
如图乙, 作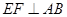 于点
于点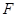 , 猜想
, 猜想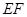 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;
如图丙, 在上述条件下, 过点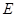 作
作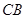 的平行线交
的平行线交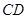 于点
于点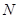 , 当
, 当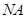 与半圆
与半圆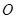 相切时, 求
相切时, 求

甲 乙
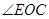 的正切值.
的正切值.
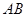 是半圆
是半圆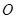 的直径, 点
的直径, 点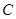 在
在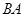 的延长线上运动(点
的延长线上运动(点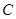 与点
与点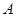 不重合), 以
不重合), 以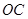 为直径的半圆
为直径的半圆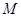 与半圆
与半圆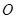 交于点
交于点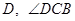 的平分线与半圆
的平分线与半圆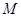 交于点
交于点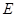 .
.如图甲, 求证:
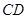 是半圆
是半圆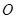 的切线;
的切线;如图乙, 作
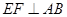 于点
于点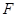 , 猜想
, 猜想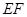 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;如图丙, 在上述条件下, 过点
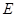 作
作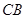 的平行线交
的平行线交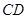 于点
于点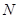 , 当
, 当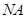 与半圆
与半圆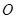 相切时, 求
相切时, 求
甲 乙
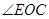 的正切值.
的正切值.角度转换;三角形全等的变换;3
试题分析:(1) 如图甲, 连接
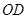 , 则
, 则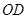 为半圆
为半圆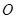 的半径, 而
的半径, 而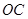 为半圆
为半圆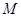 的直径, 所以
的直径, 所以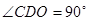 ,
,即
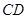 是半圆
是半圆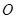 的切线;
的切线;(2) 猜想:
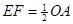 .
.证1: 如图乙, 以
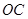 为直径作⊙
为直径作⊙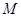 , 延长
, 延长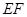 交⊙
交⊙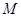 于点
于点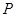 ,连接
,连接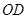 ,
, ∵
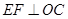 , ∴
, ∴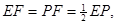 ∵
∵ 平分
平分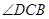 , ∴
, ∴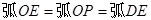 ,
,∴
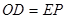 , ∴
, ∴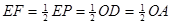 ;
;
甲 乙 丙 丁
证2: 如图丙, 连接
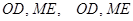 相交于点
相交于点 . ∵
. ∵ 平分
平分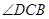 , ∴
, ∴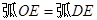 ,
,∴
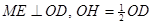 , ∴可证
, ∴可证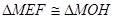 , ∴
, ∴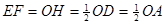 ;
;(3) 如图丁, 延长
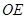 交
交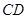 于点
于点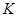 , 设
, 设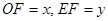 , 则
, 则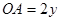 ,
, ∵四边形
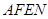 是矩形, ∴
是矩形, ∴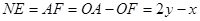 , 同(2)证法
, 同(2)证法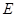 是
是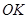 中点,
中点,∴
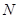 是
是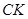 中点, ∴
中点, ∴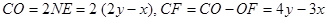 ,
,可证
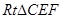 ∽
∽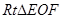 , ∴
, ∴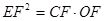 , 即
, 即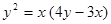 , 解得
, 解得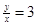 或
或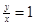 .
.当
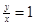 时, 点
时, 点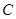 与点
与点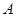 重合, 舍去; 当
重合, 舍去; 当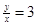 时,
时, 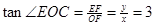 .
.点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目


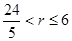

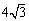 cm,则劣弧
cm,则劣弧 等于 .
等于 .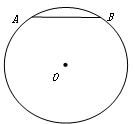
 ,BE=
,BE= ,求OE的长.
,求OE的长.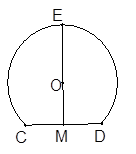
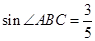 ,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
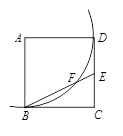
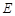 是正方形
是正方形 的边
的边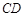 上一点,以
上一点,以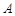 为圆心,
为圆心,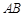 为半径的弧与
为半径的弧与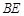 交于点
交于点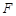 ,则
,则 .
.