题目内容
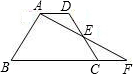
已知梯形![]() 中,AD//BC,∠A=120°,E是AB的中点,过E点作射线EF//BC,交CD于点G,AB、AD的长恰好是方程
中,AD//BC,∠A=120°,E是AB的中点,过E点作射线EF//BC,交CD于点G,AB、AD的长恰好是方程![]() 的两个相等实数根,动点P、Q分别从点A、E出发,点P以每秒1个单位长度的速度沿射线AB由点
的两个相等实数根,动点P、Q分别从点A、E出发,点P以每秒1个单位长度的速度沿射线AB由点![]() 向点B运动,点Q以每秒2个单位长度的速度沿EF由E向F运动,设点P、Q运动的时间为t.
向点B运动,点Q以每秒2个单位长度的速度沿EF由E向F运动,设点P、Q运动的时间为t.
(1)求线段AB、AD的长;
(2)如果t > 1,DP与EF相交于点N,求![]() 的面积S与时间t之间的函数关系式.
的面积S与时间t之间的函数关系式.
(3)当t >0时,是否存在![]() 是直角三角形的情况,如果存在请求出时间t ,如果不存在,说明理由.
是直角三角形的情况,如果存在请求出时间t ,如果不存在,说明理由.

解:根据题意可知,![]()
![]()
![]()
![]() 原方程可化为:
原方程可化为:![]()
![]()
![]()
![]()
![]()
(2) 过点P作PM![]() DA,交DA的延长线于M,过点D作DK
DA,交DA的延长线于M,过点D作DK![]() EF
EF
 |
![]()
![]() ,AD//BC且
,AD//BC且![]()
![]()
![]() ,
,![]()
![]() E是AB中点,且EF//BC,
E是AB中点,且EF//BC,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() 是AB中点,AD//EF,AB=2,
是AB中点,AD//EF,AB=2,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
(3)根据题意可知:![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() 根据勾股定理可得:
根据勾股定理可得:![]()
![]() ,
,![]()
![]() ,当
,当![]() ,
,![]() ,
,![]() =
=![]() +
+![]()
解之得:![]() (舍负)
(舍负)
① 当![]()
![]() ,
,![]() =
=![]() +
+![]()
解之得:![]() (舍负)
(舍负)
② 当![]() ,
,![]() ,
,![]() =
=![]() +
+![]()
解之得:![]()
综上,当![]() ,
,![]() ,
,![]() 时
时![]() 是直角三角形.
是直角三角形.

练习册系列答案
相关题目
 10、如图,已知梯形ABCD,AD∥BC,AF交CD于E,交BC的延长线于F.
10、如图,已知梯形ABCD,AD∥BC,AF交CD于E,交BC的延长线于F.