题目内容
如图，将△ABC沿直线AC翻折得到△AB′C，若∠BAC=25°，则∠AB′B=65
65
度．分析：根据翻折变换的性质得出∠B′AC=25°，AB=AB′，进而得出∠ABB′=∠AB′B，再利用三角形内角和求出即可．
解答：
解：连接BB′，
∵将△ABC沿直线AC翻折得到△AB′C，∠BAC=25°，
∴∠B′AC=25°，AB=AB′，
∴∠ABB′=∠AB′B，
∴2∠AB′B=180°-25°-25°=130°，
∴∠AB′B=65°，
故答案为：65．
解：连接BB′，∵将△ABC沿直线AC翻折得到△AB′C，∠BAC=25°，
∴∠B′AC=25°，AB=AB′，
∴∠ABB′=∠AB′B，
∴2∠AB′B=180°-25°-25°=130°，
∴∠AB′B=65°，
故答案为：65．
点评：此题主要考查了翻折变换的性质，根据已知得出∠ABB′=∠AB′B是解题关键．
练习册系列答案
相关题目
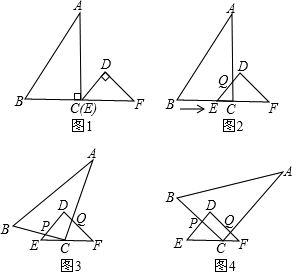已知：RT△ABC与RT△DEF中，∠ACB=∠EDF=90°，∠DEF=45°，EF=8cm，AC=16cm，BC=12cm．现将RT△ABC和RT△DEF按图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，并按如下方式运动．
，当QC⊥DF时暂停旋转；