题目内容
如图：在△ABC中，点M是BC上任一点，MD∥AC，ME∥AB，| BD |
| AB |
| 2 |
| 5 |
| CE |
| AC |
考点：相似三角形的判定与性质
专题：
分析：由MD∥AB，可证明△CEM∽△BAC，利用相似三角形的性质即可求出CE：AC的值．
解答：证明：∵MD∥AB，
∴△CEM∽△BAC，
∴
=
=
，
=
又∵ME∥AB，
∴△CEM∽△CAB，
∴
=
=
．
∴△CEM∽△BAC，
∴
| BD |
| BA |
| BM |
| BC |
| 2 |
| 5 |
| MC |
| BC |
| 3 |
| 5 |
又∵ME∥AB，
∴△CEM∽△CAB，
∴
| CE |
| CA |
| CM |
| CB |
| 3 |
| 5 |
点评：本题考查了相似三角形的判定和性质，是中考常见题型，比较简单．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
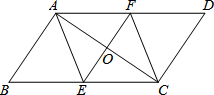如图，在?ABCD中，EF垂直平分AC交BC于E，交AD于F．
如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
如图所示，直角坐标系内，A（-4，3），B（-2，0），C（-1，2），请你在图中画出△ABC关于原点O的对称的图形即△A′B′C′，并写出A′、B′、C′的坐标，求出△A′B′C′的面积．
如图，一次函数y=y=-2x-4的图象分别与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC=90°，求过B、C两点直线的解析式．
如图，在平面内有A、B、C三点．