Question

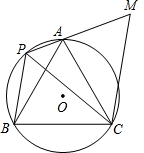如图，A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°，过点C作CM∥BP交PA的延长线于点M．
（1）求证：△ACM≌△BCP；
（2）若PA=1，PB=2，求△PCM的面积．

Answer 1

分析：（1）根据圆周角定理由∠APC=∠CPB=60°得∠BAC=∠ABC=60°，则△ABC是等边三角形，所以BC=AC，∠ACB=60°，再由CM∥BP得到∠PCM=∠BPC=60°，有可判断△PCM是等边三角形，得到PC=MC，∠M=60°，易得∠PCB=∠ACM，然后利用“AAS“可判断△ACM≌△BCP≌△ACM；
（2）由△ACM≌△BCP≌△ACM得AM=PB=2，则PM=PA+AM=3，由于△PCM是等边三角形，于是可根据等边三角形的性质计算其面积．

解答：（1）证明：∵∠APC=∠CPB=60°，
∴∠BAC=∠ABC=60°，
∴△ABC是等边三角形，
∴BC=AC，∠ACB=60°，
∵CM∥BP
∴∠PCM=∠BPC=60°，
又∵∠APC=60°，
∴△PCM是等边三角形
∴PC=MC，∠M=60°，
∵∠BCA-∠PCA=∠PCM-∠PCA，
∴∠PCB=∠ACM，
在△ACM和△BCP中，

∠BPC=∠M ∠PCB=∠MCA CB=CA

，
∴△ACM≌△BCP≌△ACM（AAS），

（2）∵△ACM≌△BCP，
∴AM=PB=2，
∴PM=PA+AM=1+2=3，
∵△PCM是等边三角形，
∴△PCM的面积=

3

4

CM²=

9 3

4

．

点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等边三角形的判定与性质、三角形全等的判定与性质．