��Ŀ����
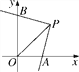
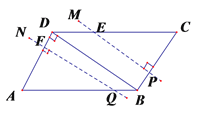
����Ŀ����ͼ������ABCD�У�AD=4cm����A=60����BD��AD.һ����P��A��������ÿ��1cm���ٶ���A��B��C��·�������˶�������P��ֱ��PM��ʹPM��AD.
��1������P�˶�2��ʱ����ֱ��PM��AD�ཻ�ڵ�E������APE�������
��2������P�˶�2��ʱ����һ����QҲ��A������A��B��·���˶�������AB����ÿ��1cm���ٶ������˶�������P��Q�е�ijһ�㵽���յ㣬�����㶼ֹͣ�˶�.����Q��ֱ��QN��ʹQN��PM�����Q�˶���ʱ��Ϊt�루0��t��8����ֱ��PM��QN����ABCD����ͼ�ε����ΪS��cm2��.��S����t�ĺ�����ϵʽ.

���𰸡���1��![]() ����2��
����2��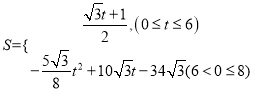 .
.
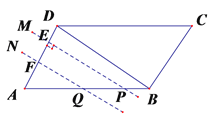
�����������������(1)����������ó�AP=2AE�������t=2ʱAP��AE��PE�ij��ȣ��Ӷ������APE�������(2)������P��AB��ʱ���Եó�AQ=t��AP=t+2�� ![]() ��
�� ![]() ��
�� ![]() �Ӷ�����ı���PQFE�����������P��BC��ʱ������
�Ӷ�����ı���PQFE�����������P��BC��ʱ������![]() �ó���������ʽ��
�ó���������ʽ��
���������(1)����A=60����PE��AD ��AP=2AE��
t=2ʱ��AP=2��AE=1��PE=![]() �� ��
�� ��![]() ��
��
(2)����![]() ʱ��P��AB��
ʱ��P��AB��
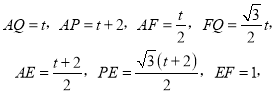
![]()
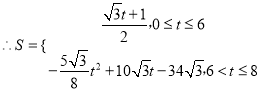 ��
��
���������������Ҫ������Ƕ��������뺯��ͼ�����⣬�Ѷ����ϣ��ڽ���йض��������ʱ������һ��Ҫע����з������ۣ���ÿһ��ȡֵ��Χ֮�ڣ�����Ҫ�����е��߶��ú�δ֪���Ĵ���ʽ�����б�ʾ��Ȼ���������ļ��㷨���������������ʽ�������ڷ������۵�ʱ����Զ������ͼ�Σ�Ȼ��ֱ���м��㣮

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�