题目内容
如图,有一座抛物线形拱桥,正常水位时桥下水面宽度为20米,拱顶距离水面4米.某天受暴雨影响,水位上涨了0.5米,则水面宽度减少了 米.


考点:二次函数的应用
专题:
分析:先运用待定系数法求出抛物线的解析式,再将y=-3.5代入解析式就可以求出水面的宽度,就可以求出结论.
解答:解:设抛物线的解析式为y=ax2,A(-10,-4,),B(10,-4),由题意,得
-4=100a,
∴a=-
.
∴y=-
x2,
当y=-3.5时,
-3.5=-
x2,
解得:x1=
,x2=-
,
∴水面的宽度为:5
,
∴水面宽度减少了(20-5
)米.
故答案为:(20-5
)
-4=100a,
∴a=-
| 1 |
| 25 |
∴y=-
| 1 |
| 25 |
当y=-3.5时,
-3.5=-
| 1 |
| 25 |
解得:x1=
5
| ||
| 2 |
5
| ||
| 2 |
∴水面的宽度为:5
| 14 |
∴水面宽度减少了(20-5
| 14 |
故答案为:(20-5
| 14 |
点评:本题考查了待定系数法求二次函数的解析式,由函数值求自变量的值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
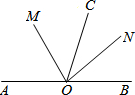 已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由.
已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由. 如图,∠B=30°,∠C=70°,则∠CAD=
如图,∠B=30°,∠C=70°,则∠CAD=