题目内容
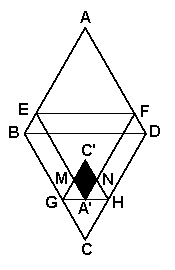
已知菱形纸片ABCD的边长为8,∠A=60°,E为AB边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点A'处,过点A'作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点C'处,C'G与C'H分别交A'E与A'F于点M、N.若点C'在△A'EF的内部或边上,此时我们称四边形A'MC'N(即图中阴影部分)为“重叠四边形”.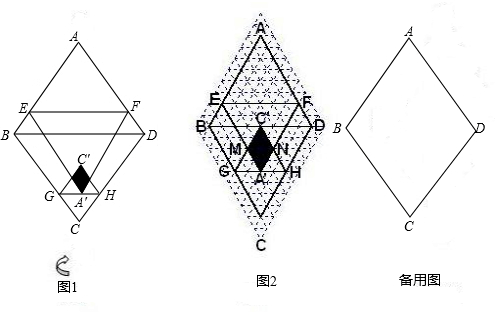
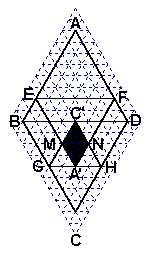
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形A'MC'N的面积;
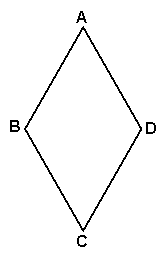
(2)实验探究:设AE的长为m,若重叠四边形A'MC'N存在.试用含m的代数式表示重叠四边形A'MC'N的面积,并写出m的取值范围(直接写出结果,备用图供实验,探究使用).
解:(1)重叠四边形A'MC'N的面积为
(2)用含m的代数式表示重叠四边形A'MC'N的面积为
分析:(1)由折叠的性质,即可证得四边形A′MC′N是菱形,然后由A′M=2,∠A′=60°,即可求得MN=2,A′C′=2
,根据菱形的面积等于对角线积的一半,即可求得重叠四边形A′MC′N的面积;
(2)首先由折叠的性质,证得A′M=GM=BE,然后由AE=m,则A′M=8-m,根据(1)的方法,即可求得用含m的代数式表示重叠四边形A′MC′N的面积.
| 3 |
(2)首先由折叠的性质,证得A′M=GM=BE,然后由AE=m,则A′M=8-m,根据(1)的方法,即可求得用含m的代数式表示重叠四边形A′MC′N的面积.
解答:解:(1)根据题意得:∠A′=∠C′=60°,∠C′MA′=∠C′NA′=120°,
∴四边形A′MC′N是平行四边形,
∵A′M=C′M,
∴四边形A′MC′N是菱形,
∵A′M=2,∠A′=60°,
∴MN=2,A′C′=2
,
∴重叠四边形A′MC′N的面积为:
MN•A′C′=
×2×2
=2
;(2分)
(2)根据题意得:BE∥GM,BC∥A′E,
∴四边形BEMG是平行四边形,
∴GM=BE,
∵∠MGA′=∠A′MG=60°,
∴△A′GM是等边三角形,
∴A′M=GM=BE,
∵AE=m,则A′M=8-m,
由(1)得:MN=8-m,A′C′=
(8-m),
∴用含m的代数式表示重叠四边形A′MC′N的面积为
(8-m)2;(4分)
∴m的取值范围为
≤m<8.(5分)
∴四边形A′MC′N是平行四边形,
∵A′M=C′M,
∴四边形A′MC′N是菱形,
∵A′M=2,∠A′=60°,
∴MN=2,A′C′=2
| 3 |
∴重叠四边形A′MC′N的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)根据题意得:BE∥GM,BC∥A′E,
∴四边形BEMG是平行四边形,
∴GM=BE,
∵∠MGA′=∠A′MG=60°,
∴△A′GM是等边三角形,
∴A′M=GM=BE,
∵AE=m,则A′M=8-m,
由(1)得:MN=8-m,A′C′=
| 3 |
∴用含m的代数式表示重叠四边形A′MC′N的面积为
| ||
| 2 |
∴m的取值范围为
| 16 |
| 3 |
点评:此题考查了折叠的性质,平行四边形的判定与性质,以及菱形的性质等知识.此题图形较复杂,难度适中,解此题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本小题满分5分)已知菱形纸片ABCD的边长为 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点 处,
处, 与
与 H分别交
H分别交 与
与 于点M、N.若点
于点M、N.若点 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.



图1 图2 备用图
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形 的面积;
的面积;
(2)实验探究:设AE的长为 ,若重叠四边形
,若重叠四边形 存在.试用含
存在.试用含 的代数式表示重叠四边形
的代数式表示重叠四边形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点 处,
处, 与
与 H分别交
H分别交 与
与 于点M、N.若点
于点M、N.若点 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.


 | |||
 | |||
图1 图2 备用图
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形
 的面积;
的面积;(2)实验探究:设AE的长为
 ,若重叠四边形
,若重叠四边形 存在.试用含
存在.试用含 的代数式表示重叠四边形
的代数式表示重叠四边形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用). 


 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 处,
处,
 与
与 与
与 于点M、N.若点
于点M、N.若点 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.


 ,若重叠四边形
,若重叠四边形