题目内容
解方程组:(1) ;(2)
;(2) ;(3)
;(3)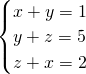 .
.
解:(1)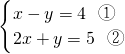
①+②得:3x=9
解得:x=3
把x=3代入①得:y=-1
所以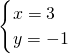 ;
;
(2)原方程可化为
①×4-②×3得:7x=42
解得:x=6
把x=6代入①得:y=4
所以 ;
;
(3)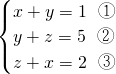
把③变为z=2-x
把z代入上两式得: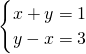
两式相加得:2y=4
解得:y=2
把y=2代入①得:x=-1,z=3
所以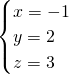 .
.
分析:这三道题都用加减法,先把y(x)的系数转化成相同的或相反的数,然后两式相加减消元,从而求出x(y)的值,然后把x的值代入一方程求y(x)的值.
点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元,消元的方法有代入法和加减法.
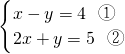
①+②得:3x=9
解得:x=3
把x=3代入①得:y=-1
所以
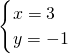 ;
;(2)原方程可化为

①×4-②×3得:7x=42
解得:x=6
把x=6代入①得:y=4
所以
 ;
;(3)
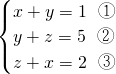
把③变为z=2-x
把z代入上两式得:
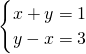
两式相加得:2y=4
解得:y=2
把y=2代入①得:x=-1,z=3
所以
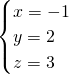 .
.分析:这三道题都用加减法,先把y(x)的系数转化成相同的或相反的数,然后两式相加减消元,从而求出x(y)的值,然后把x的值代入一方程求y(x)的值.
点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元,消元的方法有代入法和加减法.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: