题目内容
若1+x+x2+x3=0，求x+x2+x3+x4+x5+x6+x7+x8的值．
考点：因式分解的应用
专题：
分析：利用已知将上式分组，进而分解因式得出即可．
解答：解：∵1+x+x2+x3=0，
∴x+x2+x3+x4+x5+x6+x7+x8
=x（1+x+x2+x3）+x5（1+x+x2+x3）
=0+0
=0．
∴x+x2+x3+x4+x5+x6+x7+x8
=x（1+x+x2+x3）+x5（1+x+x2+x3）
=0+0
=0．
点评：此题主要考查了因式分解的应用，正确利用分组分解因式是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知点P是半径为1.5的⊙A上一点，延长AP到C，使PC=AP，以AC为对角线作?ABCD．若AB=2，则?ABCD面积的最大值为
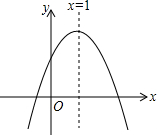二次函数y=ax2+bx+c（a≠0）图象如图所示，现有下列结论：①b2-4ac＞0；②a＞0；③b＞0；④c＞0；⑤4a+2b+c＜0，则其中结论正确的个数是（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
在Rt△ABC中，∠C=90°，AB=5，BC=2，则cosA的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面直角坐标系内与点P关于原点对称的点的坐标为（2，-3），则点P的坐标为（ ）
| A、（-2，3） |
| B、（-2，-3） |
| C、（-3，2） |
| D、（2，3） |