题目内容
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是平行四边形,点
是平行四边形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的动点,若
上的动点,若![]() 是等腰三角形,则点
是等腰三角形,则点![]() 的坐标为_____.
的坐标为_____.

【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
分三种情形讨论求解即可:①当EP=EB时,②当BP=BE时,③当PB=PE时.
解:①当EP=EB时,
如图1,作EH⊥AD于H,则四边形OAHE是矩形.
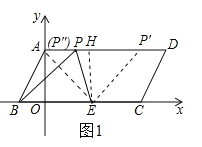
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=EH=2,BC=5,
∵点![]() 是
是![]() 的中点,
的中点,
∴BE=2.5,OE=AH=1.5,
PH=![]() =1.5,
=1.5,
当点P在点H左侧时,P″(0,2),当点P在点H右侧时,P′(3,2);
②当BP=BE时,
如图2,作PF⊥BC于F,则四边形OAPF是矩形,
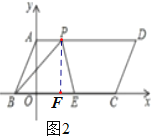
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=PF=2,BC=5,
∵点![]() 是
是![]() 的中点,
的中点,
∴BE=2.5,OE =1.5,
∴OF=AP=0.5,
∴P(0.5,2);
③当PB=PE时,如图2,
∵PB=PE,PF⊥BC,
∴BF=![]() =1.25,
=1.25,
∴OF=0.25,
∴P(0.25,2);
综上所述,满足条件的点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目





