题目内容
在-
,-2,
,
,3.14,
,(
)0中有理数的个数是( )
| π |
| 3 |
| 4 |
| ||
| 2 |
| 22 |
| 3 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
分析:实数的判断,先化简,后根据实数的值和有理数的范围进行判断.
解答:解:有理数有-2,
=2,3.14,
,(
)0=1.
所以有理数的个数是5个.故选D.
| 4 |
| 22 |
| 3 |
| 2 |
所以有理数的个数是5个.故选D.
点评:(1)有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,例如5=5.0;分数都可以化为有限小数或无限循环小数;
(2)无理数是无限不循环小数,其中有开方开不尽的数,如2,33等,也有π这样的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来表示;而无限不环小数不能化为分数,它是无理数.
(2)无理数是无限不循环小数,其中有开方开不尽的数,如2,33等,也有π这样的数.
(3)有限小数和无限循环小数都可以化为分数,也就是说,一切有理数都可以用分数来表示;而无限不环小数不能化为分数,它是无理数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
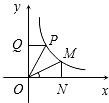 设P(a,b),M(c,d)是反比例函数y=
设P(a,b),M(c,d)是反比例函数y=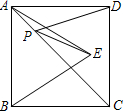 如图所示,正方形ABCD的面积为18,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为18,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( ) 20、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.
20、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.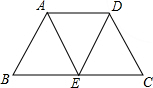 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?