题目内容
 右图是四分之一圆,半径OA,OB互相垂直,AO=1,点C在弧AB上,且
右图是四分之一圆,半径OA,OB互相垂直,AO=1,点C在弧AB上,且 =2
=2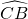 .若点P是半径OB上一个动点,那么AP+PC的最小值是
.若点P是半径OB上一个动点,那么AP+PC的最小值是
- A.3
- B.

- C.

- D.3

C
分析:首先可以把四分之一圆扩充成半圆,此时有直径AD,根据轴对称的知识,知连接CD交圆于点P,此时AP+PC最小且等于CD.
解答: 解:连接AC,
解:连接AC,
根据直径所对的圆周角是直角,得∠ACD=90°,
根据题意,得∠D=30°,
则CD= .
.
故选C.
点评:解决此题的重点是根据对称的知识确定点P的位置.发现一个特殊的直角三角形,根据直角三角形的性质求解.
分析:首先可以把四分之一圆扩充成半圆,此时有直径AD,根据轴对称的知识,知连接CD交圆于点P,此时AP+PC最小且等于CD.
解答:
 解:连接AC,
解:连接AC,根据直径所对的圆周角是直角,得∠ACD=90°,
根据题意,得∠D=30°,
则CD=
 .
.故选C.
点评:解决此题的重点是根据对称的知识确定点P的位置.发现一个特殊的直角三角形,根据直角三角形的性质求解.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目