Question

如图，在?ABCD中，E是AD上一点，连接BE，F为BE中点，且AF=BF，

（1）求证：四边形ABCD为矩形；

（2）过点F作FG⊥BE，垂足为F，交BC于点G，若BE=BC，S△BFG=5，CD=4，求CG．

 

Answer 1

（1）证明见解析；（2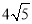）-5．

【解析】

试题分析：（1）求出∠BAE=90°，根据矩形的判定推出即可；

（2）求出△BGE面积，根据三角形面积公式求出BG，得出EG长度，根据勾股定理求出GH，求出BE，得出BC长度，即可求出答案．

试题解析：（1）证明：∵F为BE中点，AF=BF，

∴AF=BF=EF，

∴∠BAF=∠ABF，∠FAE=∠AEF，

在△ABE中，∠BAF+∠ABF+∠FAE+∠AEF=180°，

∴∠BAF+∠FAE=90°，

又四边形ABCD为平行四边形，

∴四边形ABCD为矩形；

（2）【解析】
连接EG，过点E作EH⊥BC，垂足为H，

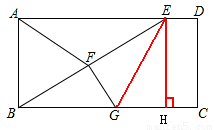
∵F为BE的中点，FG⊥BE，

∴BG=GE，

∵S△BFG=5，CD=4，

∴S△BGE=10=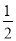BG•EH，

∴BG=GE=5，

在Rt△EGH中，GH=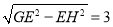

在Rt△BEH中，BE=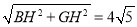=BC，

∴CG=BC-BG=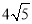-5．

考点：1.矩形的判定与性质；2.勾股定理；3.平行四边形的性质．