题目内容
如图，在Rt△ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三角形．若AB=2，求△ABC的周长．（结果保留根号）
解：∵△ABD是等边三角形，
∴∠B=60°，
∵∠BAC=90°，
∴∠C=180°﹣90°﹣60°=30°，
∴BC=2AB=4，
在Rt△ABC中，由勾股定理得：AC=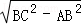
=
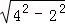=2
，
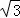∴△ABC的周长是AC+BC+AB=2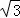+4+2=6+2．
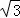答：△ABC的周长是6+2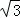
．
解析
练习册系列答案
相关题目
题目内容
如图，在Rt△ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三角形．若AB=2，求△ABC的周长．（结果保留根号）
解：∵△ABD是等边三角形，
∴∠B=60°，
∵∠BAC=90°，
∴∠C=180°﹣90°﹣60°=30°，
∴BC=2AB=4，
在Rt△ABC中，由勾股定理得：AC=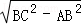==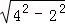2，
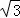∴△ABC的周长是AC+BC+AB=2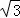+4+2=6+2．
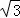答：△ABC的周长是6+2．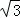
解析
（2013•莆田质检）如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D，点E是AB上一点，以AE为直径的⊙O过点D，且交AC于点F．
如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，AD和BD分别是∠BAC和∠ABC的平分线，它们相交于点D，求点D到BC的距离．
边上移动，使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F，且使DE始终与AB垂直．
如图，在Rt△ABC中，BD⊥AC，sinA=
点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t（s）．