题目内容
求下列函数的图象的对称轴、顶点坐标及与x轴的交点坐标.(1)y=4x2+24x+35;(2)y=-3x2+6x+2;(3)y=x2-x+3;(4)y=2x2+12x+18.
【答案】分析:因为二次函数y=ax2+bx+c的对称轴为x=- ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0.
所以代入公式,求解即可.
解答:解:(1)∵y=4x2+24x+35,
∴对称轴是直线x=-3,顶点坐标是(-3,-1),
解方程4x2+24x+35=0,
得x1= ,x2=
,x2= ,
,
故它与x轴交点坐标是( ,0),(
,0),( ,0);
,0);
(2)∵y=-3x2+6x+2,
∴对称轴是直线x=1,顶点坐标是(1,5),
解方程-3x2+6x+2=0,
得 ,
,
故它与x轴的交点坐标是 ;
;
(3)∵y=x2-x+3,
∴对称轴是直线x= ,顶点坐标是
,顶点坐标是 ,
,
解方程x2-x+3=0,无解,
故它与x轴没有交点;
(4)∵y=2x2+12x+18,
∴对称轴是直线x=-3,顶点坐标是(-3,0),
当y=0时,2x2+12x+18=0,
∴x1=x2=-3,
∴它与x轴的交点坐标是(-3,0).
点评:此题考查了二次函数的性质:二次函数y=ax2+bx+c的对称轴为x=- ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0.
 ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0.所以代入公式,求解即可.
解答:解:(1)∵y=4x2+24x+35,
∴对称轴是直线x=-3,顶点坐标是(-3,-1),
解方程4x2+24x+35=0,
得x1=
 ,x2=
,x2= ,
,故它与x轴交点坐标是(
 ,0),(
,0),( ,0);
,0);(2)∵y=-3x2+6x+2,
∴对称轴是直线x=1,顶点坐标是(1,5),
解方程-3x2+6x+2=0,
得
 ,
,故它与x轴的交点坐标是
 ;
;(3)∵y=x2-x+3,
∴对称轴是直线x=
 ,顶点坐标是
,顶点坐标是 ,
,解方程x2-x+3=0,无解,
故它与x轴没有交点;
(4)∵y=2x2+12x+18,
∴对称轴是直线x=-3,顶点坐标是(-3,0),
当y=0时,2x2+12x+18=0,
∴x1=x2=-3,
∴它与x轴的交点坐标是(-3,0).
点评:此题考查了二次函数的性质:二次函数y=ax2+bx+c的对称轴为x=-
 ,顶点坐标为(-
,顶点坐标为(- ,
, ),与x轴的交点的纵坐标为0.
),与x轴的交点的纵坐标为0. 
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
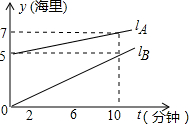 、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:
、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题: 、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题:
、lB分别表示y2、y1与t之间的关系.结合图象回答下列问题: