题目内容
(2009•湛江)某语文老师为了了解中考普通话考试的成绩情况,从所任教的九年级(1)、(2)两班各随机抽取了10名学生的得分,如图所示: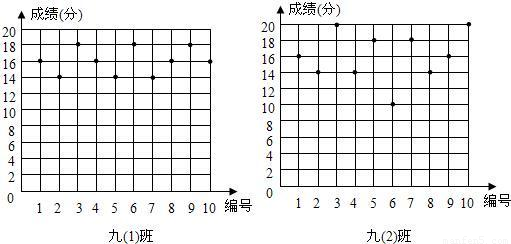
(1)利用图中的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1)班 | 16 | 16 | |
| 九(2)班 | 16 |
【答案】分析:(1)从表中可以看出10名学生的得分分别是16,14,18,16,14,18,14,16,18,16,求平均数即可,九年级二班的学生得分分别是16,14,20,14,18,10,18,14,16,20,按从小到大的顺序排列得10,14,14,14,16,16,18,18,20,20,由此即可求出答案;
(2)用样本中的优秀率去估计两班的优秀率.
解答:解:(1)
(6分)
(2)∵60× =42(名),60×
=42(名),60× =36(名).
=36(名).
∴九(1)班有42名学生成绩优秀,九(2)班有36名学生成绩优秀.(10分)
点评:从不同的统计图中得到必要的信息是解决问题的关键.除此之外,本题也考查了平均数、中位数、众数的知识.
(2)用样本中的优秀率去估计两班的优秀率.
解答:解:(1)
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1)班 | 16 | 16 | 16 |
| 九(2)班 | 16 | 16 | 14 |
(2)∵60×
 =42(名),60×
=42(名),60× =36(名).
=36(名).∴九(1)班有42名学生成绩优秀,九(2)班有36名学生成绩优秀.(10分)
点评:从不同的统计图中得到必要的信息是解决问题的关键.除此之外,本题也考查了平均数、中位数、众数的知识.

练习册系列答案
相关题目
(2009•湛江)某语文老师为了了解中考普通话考试的成绩情况,从所任教的九年级(1)、(2)两班各随机抽取了10名学生的得分,如图所示:
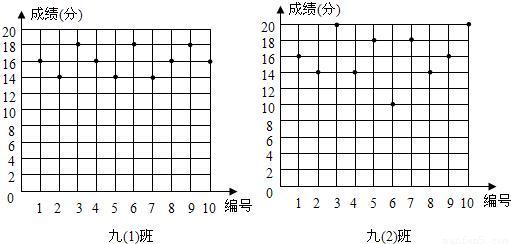
(1)利用图中的信息,补全下表:
(2)若把16分以上(含16分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀.

(1)利用图中的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1)班 | 16 | 16 | |
| 九(2)班 | 16 |
(2009•湛江)某语文老师为了了解中考普通话考试的成绩情况,从所任教的九年级(1)、(2)两班各随机抽取了10名学生的得分,如图所示:
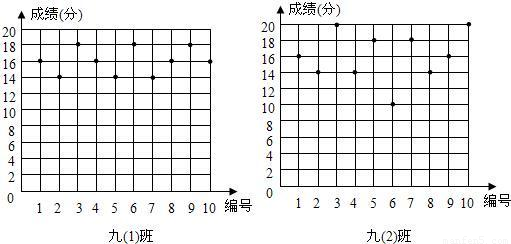
(1)利用图中的信息,补全下表:
(2)若把16分以上(含16分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀.

(1)利用图中的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1)班 | 16 | 16 | |
| 九(2)班 | 16 |
(2009•湛江)某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:
(1)设生产甲种产品x件,根据题意列出不等式组,求出x的取值范围;
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,写出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.
| 原料 含量 产品 | A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,写出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.
(2009•湛江)某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:
(1)设生产甲种产品x件,根据题意列出不等式组,求出x的取值范围;
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,写出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.
| 原料 含量 产品 | A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,写出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各生产多少件时,产品的成本总额最少?并求出最少的成本总额.