题目内容
已知矩形ABCD中,如图,对角线AC、BD相交于O,AE⊥BD于E,若∠DAE∶∠BAE=3∶1,则∠EAC=________.

【答案】
45°
【解析】
试题分析:由∠DAE:∠BAE=3:1,可得∠BAE的大小,进而得出∠ABE的大小,又OA=OB,进而可求∠EAC的大小.
如图
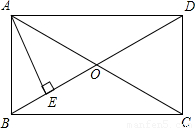
∵∠DAE:∠BAE=3:1,
∴∠BAE=22.5°,
∴∠ABE=67.5°,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO
∴OA=OB,
∴∠OAB=∠ABE=67.5°
∴∠EAC=∠OAB-∠BAE=67.5°-22.5°=45°.
考点:本题主要考查了矩形的性质
点评:解答本题的关键是熟练掌握矩形的性质,能够求解一些简单的角度计算问题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
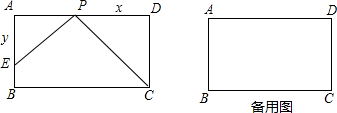
 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
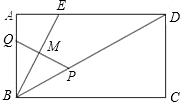
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.