Question

(本小题满分12分)
在平面直角坐标系xOy中，抛物线的解析式是y =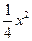+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.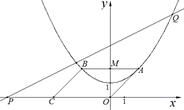

(1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值.

Answer 1

（1）M (0，2)
（2）①t = –+ x –2
②–8.

解析(1) ∵OABC是平行四边形，∴AB∥OC，且AB =" OC" = 4，
∵A，B在抛物线上，y轴是抛物线的对称轴，
∴ A，B的横坐标分别是2和– 2，
代入y =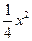+1得， A(2, 2 )，B(– 2，2)，
∴M (0，2)，                                            ---2分
(2) ① 过点Q作QH ^ x轴，设垂足为H， 则HQ =" y" ，HP =" x–t" ，
由△HQP∽△OMC，得：, 即： t =" x" – 2y ,
∵ Q(x,y) 在y = 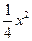+1上，
∴ t = –+ x –2.                        ---2分
当点P与点C重合时，梯形不存在，此时，t =" –" 4，解得x = 1±,
当Q与B或A重合时，四边形为平行四边形，此时，x = ± 2
∴x的取值范围是x ¹ 1±,
且x¹± 2的所有实数.                         ---2分
② 分两种情况讨论：
1）当CM > PQ时，则点P在线段OC上，                                                            
∵ CM∥PQ，CM =" 2PQ" ，
∴点M纵坐标为点Q纵坐标的2倍，即2 = 2(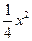+1)，解得x =" 0" ，
∴t = –+ 0 –2
=" –2 " .                                             --- 2分
2）当CM < PQ时，则点P在OC的延长线上，
∵CM∥PQ，CM = PQ，
∴点Q纵坐标为点M纵坐标的2倍，即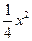+1=2´2，解得： x = ±.     ---2分                                                 
当x = –时，得t = –––2 =" –8" –,                       
当x =时，
得t =–8.                                  ---2分