Question

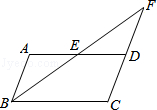
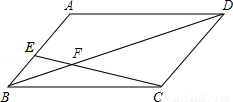
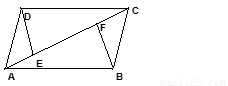
如图，在▱ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过A点作AG∥BD交CB的延长线于点G.

(1)求证：DE∥BF；

(2)若∠G＝90°，求证：四边形DEBF是菱形．

Answer 1

解　(1)证明：在▱ABCD中，AB∥CD，AB＝CD.

∵E、F分别为边AB、CD的中点，

∴DF＝DC，BE＝AB，

∴DF∥BE，DF＝BE.

∴四边形DEBF为平行四边形．

∴DE∥BF.

(2)证明： ∵AG∥BD，

∴∠G＝∠DBC＝90°.

∴△DBC为直角三角形．

又∵F为边CD的中点，

∴BF＝CD＝DF.

又∵四边形DEBF为平行四边形，

∴四边形DEBF是菱形．