题目内容
已知:抛物线y=ax2+bx+c与x轴交于点A(-2,0)、B(8,0),与y轴交于点C(0,-4).直线y=x+m与抛物线交于点D、E(D在E的左侧),与抛物线的对称轴交于点F.(1)求抛物线的解析式;
(2)当m=2时,求∠DCF的大小;
(3)若在直线y=x+m下方的抛物线上存在点P,使得∠DPF=45°,且满足条件的点P只有两个,则m的值为
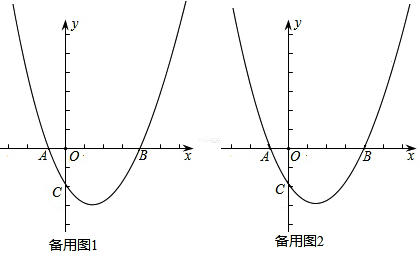
分析:(1)已知抛物线过A(-2,0)、B(8,0)两点,可设交点式y=a(x+2)(x-8),再将点C(0,-4)代入求a即可;
(2)由抛物线解析式可知对称轴为x=3,与y轴的交点(0,-4),可求MC的长,y=x+2,可知D、F两点坐标,计算DM,FM,判断C、D、F三点在以M为圆心的圆上,利用圆周角定理求∠DCF的大小;
(3)当直线y=x+m下方的抛物线上存在点P,使得∠DPF=45°,且满足条件的点P只有两个时,仿照(2)可求满足条件的m的值.
(2)由抛物线解析式可知对称轴为x=3,与y轴的交点(0,-4),可求MC的长,y=x+2,可知D、F两点坐标,计算DM,FM,判断C、D、F三点在以M为圆心的圆上,利用圆周角定理求∠DCF的大小;
(3)当直线y=x+m下方的抛物线上存在点P,使得∠DPF=45°,且满足条件的点P只有两个时,仿照(2)可求满足条件的m的值.
解答:解:(1)依题意,设抛物线的解析式为y=a(x+2)(x-8),
∵抛物线与y轴交于点C(0,-4),
∴-4=a(0+2)(0-8).
解得a=
.
∴抛物线的解析式为y=
(x+2)(x-8),即y=
x2-
x-4;
(2)由(1)可得抛物线的对称轴为x=3,
∵m=2,
∴直线的解析式为y=x+2,
∵直线y=x+2与抛物线交于点D、E,与抛物线的对称轴交于点F,
∴F、D两点的坐标分别为F(3,5),D(-2,0).
设抛物线的对称轴与x轴的交点为M,
可得CM=FM=MD=5,
∴F、D、C三点在以M为圆心,半径为5的圆上.
∴∠DCF=
∠DMF=45°.
(3)由抛物线解析式可知,抛物线顶点坐标为G(3,-
)
设F(3,3+m),则FG=m+3+
,设D关于对称轴的对称点为D1,
当四边形DGD1F为正方形时,满足题意,此时P点与顶点G重合,或者与D1重合,
故DD1=F′G,D点横坐标为:x=-(
F′G-3)=-
,纵坐标为-(
F′G-3-m)=
,
将D点坐标抛物线解析式,解得m=-
.

∵抛物线与y轴交于点C(0,-4),
∴-4=a(0+2)(0-8).
解得a=
| 1 |
| 4 |
∴抛物线的解析式为y=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
(2)由(1)可得抛物线的对称轴为x=3,
∵m=2,
∴直线的解析式为y=x+2,
∵直线y=x+2与抛物线交于点D、E,与抛物线的对称轴交于点F,
∴F、D两点的坐标分别为F(3,5),D(-2,0).
设抛物线的对称轴与x轴的交点为M,
可得CM=FM=MD=5,
∴F、D、C三点在以M为圆心,半径为5的圆上.
∴∠DCF=
| 1 |
| 2 |
(3)由抛物线解析式可知,抛物线顶点坐标为G(3,-
| 25 |
| 4 |
设F(3,3+m),则FG=m+3+
| 25 |
| 4 |
当四边形DGD1F为正方形时,满足题意,此时P点与顶点G重合,或者与D1重合,
故DD1=F′G,D点横坐标为:x=-(
| 1 |
| 2 |
| 4m+13 |
| 8 |
| 1 |
| 2 |
| 4m-13 |
| 8 |
将D点坐标抛物线解析式,解得m=-
| 5 |
| 4 |

点评:本题考查了用待定系数法求抛物线的解析式,已知抛物线与x轴的两交点,可设交点式,综合运用圆的知识,解答抛物线中角的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
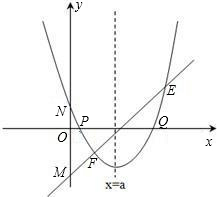 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.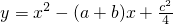 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.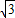 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.