题目内容
 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: (即AB:BC=1:
(即AB:BC=1: ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
 解:如图,过点A作AF⊥DE于F,
解:如图,过点A作AF⊥DE于F,则四边形ABEF为矩形,
∴AF=BE,EF=AB=3,
设DE=x,
在Rt△CDE中,CE=
 =
= x,
x,在Rt△ABC中,
∵
 =
= ,AB=3,
,AB=3,∴BC=3
 ,
,在Rt△AFD中,DF=DE-EF=x-3,
∴AF=
 =
= (x-3),
(x-3),∵AF=BE=BC+CE,
∴
 (x-3)=3
(x-3)=3 +
+ x,
x,解得x=9.
答:树高为9米.
分析:过点A作AF⊥DE于F,可得四边形ABEF为矩形,设DE=x,在Rt△DCE和Rt△ABC中分别表示出CE,BC的长度,求出DF的长度,然后在Rt△ADF中表示出AF的长度,根据AF=BE,代入解方程求出x的值即可.
点评:本题考查了解直角三角形的应用,解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上(含80分)为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,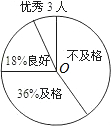 如图.
如图.
请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议;
(3)扇形图中“优秀率”是多少?
(4)“不及格”在扇形图中所占的圆心角是多少度?
(5)请从扇形图中,写出你发现的一个现象并分析其产生的原因.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上(含80分)为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,
 如图.
如图.| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
(1)小聪和小亮谁能达到“优秀毕业生”水平哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议;
(3)扇形图中“优秀率”是多少?
(4)“不及格”在扇形图中所占的圆心角是多少度?
(5)请从扇形图中,写出你发现的一个现象并分析其产生的原因.




 的值,并求出该校初一学生总数
的值,并求出该校初一学生总数
 的值,并求出该校初一学生总数
的值,并求出该校初一学生总数