题目内容
 如图,已知抛物线
如图,已知抛物线 与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2.
与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2.
(1)求二次函数解析式;
(2)若抛物线的顶点为D,联结BD并延长交y轴于点P,联结PA,求∠APC的余切值;
(3)在(2)的条件下,若抛物线上存在一点E,使得∠DPE=∠ACB,求点E坐标.
解:(1)∵抛物线 与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2,
与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2,
∴ ,
,
解得: ,
,
∴二次函数解析式为:y= x2-
x2- x+2;
x+2;
(2)∵y= x2-
x2- x+2=
x+2= (x2-4x)+2=
(x2-4x)+2= (x-2)2-
(x-2)2- ,
,
∴抛物线顶点坐标为:(2,- ),
),
设直线BD的解析式为:y=kx+a,
∴ ,
,
解得: ,
,
∴直线BD的解析式为:y= x-2,
x-2,
∴P(0,-2),
∵点B的坐标为(3,0),它的对称轴为直线x=2,
∴A点坐标为:(1,0),
在直角三角形POA中,
cot∠APC=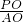 =2;
=2;
(3)∵BC=BP,AC=AP,
∴∠BCO=∠BPO,∠ACO=∠APO,
∴∠BAC=∠BPA,
∴延长PA交抛物线于点E,过点E作EH⊥x轴,
∴△AOP∽△AHE,
∴ ,
,
设AH=x,EH=2x,则点E(x+1,2x)
∴ ,
,
解得:x1=0,x2=5,
∴E1(1,0),E2(6,10).
分析:(1)利用待定系数法求二次函数解析式进而得出答案;
(2)利用配方法求出二次函数顶点坐标,进而得出A点坐标,再求出直线BD的解析式,进而得出∠APC的余切值;
(3)利用相似三角形的判定与性质得出△AOP∽△AHE,进而得出E点坐标.
点评:此题主要考查了二次函数的综合以及相似三角形的判定与性质和锐角三角函数关系等知识,根据已知结合相似三角形判定与性质得出E点坐标是解题关键.
 与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2,
与x轴交于点A、B,点B的坐标为(3,0),它的对称轴为直线x=2,∴
 ,
,解得:
 ,
,∴二次函数解析式为:y=
 x2-
x2- x+2;
x+2;(2)∵y=
 x2-
x2- x+2=
x+2= (x2-4x)+2=
(x2-4x)+2= (x-2)2-
(x-2)2- ,
,∴抛物线顶点坐标为:(2,-
 ),
),设直线BD的解析式为:y=kx+a,
∴
 ,
,解得:
 ,
,∴直线BD的解析式为:y=
 x-2,
x-2,∴P(0,-2),
∵点B的坐标为(3,0),它的对称轴为直线x=2,
∴A点坐标为:(1,0),
在直角三角形POA中,
cot∠APC=
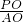 =2;
=2;
(3)∵BC=BP,AC=AP,
∴∠BCO=∠BPO,∠ACO=∠APO,
∴∠BAC=∠BPA,
∴延长PA交抛物线于点E,过点E作EH⊥x轴,
∴△AOP∽△AHE,
∴
 ,
,设AH=x,EH=2x,则点E(x+1,2x)
∴
 ,
,解得:x1=0,x2=5,
∴E1(1,0),E2(6,10).
分析:(1)利用待定系数法求二次函数解析式进而得出答案;
(2)利用配方法求出二次函数顶点坐标,进而得出A点坐标,再求出直线BD的解析式,进而得出∠APC的余切值;
(3)利用相似三角形的判定与性质得出△AOP∽△AHE,进而得出E点坐标.
点评:此题主要考查了二次函数的综合以及相似三角形的判定与性质和锐角三角函数关系等知识,根据已知结合相似三角形判定与性质得出E点坐标是解题关键.

练习册系列答案
相关题目
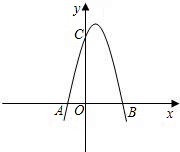 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).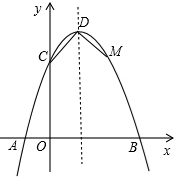 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1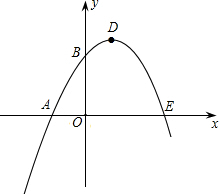 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )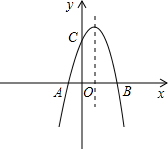 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).