题目内容
如图，一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米，太阳光线与地面的夹角∠ACD=60°，则AB的长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：依据平行于三角形一边的直线截其他两边所得的线段对应成比例及60°的正切值联立求解．
解答：
解：设直线AB与CD的交点为点O．
∴
=
．
∴AB=
．
∵∠ACD=60°．
∴∠BDO=60°．
在Rt△BDO中，tan60°=
=
．
∵CD=1．
∴AB=
×CD=
．
故选B．
解：设直线AB与CD的交点为点O．∴
| BO |
| AB |
| DO |
| CD |
∴AB=
| BO×CD |
| DO |
∵∠ACD=60°．
∴∠BDO=60°．
在Rt△BDO中，tan60°=
| BO |
| DO |
| 3 |
∵CD=1．
∴AB=
| BO |
| DO |
| 3 |
故选B．
点评：本题主要考查平行线分线段成比例定理．
练习册系列答案
阅读快车系列答案
相关题目
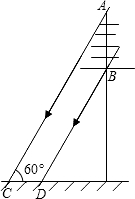如图，一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2m，太阳光线与地面的夹角∠ACD=60°，则AB的长为
如图，一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米，太阳光线与地面的夹角∠ACD=60°，则AB的长为
如图，一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.5m，太阳光线与底面的夹角∠ACD=60°，则AB的长为
米 B．
米 C．
米 D．
米