Question

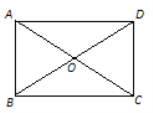
【题目】如图，在矩形ABCD中，对角线AC、BD相交于O，且AC=2AB.

（1）你能说明△AOB是等边三角形吗？请写出理由；

（2）若AB=1，求点D到AC的距离.

Answer 1

【答案】（1）△OAB是等边三角形（2）DE=

【解析】试题分析：（1）根据矩形的对角线互相平分且相等可得OA=OB，再求出AB=AC，然后根据三条边都相等的三角形是等边三角形解答；

（2）在Rt△ABC中，根据勾股定理求出BC的长， 作DE⊥AC于E，利用三角形的面积法即可求得DE长．

试题解析：（1）△OAB是等边三角形， 理由如下：

在矩形ABCD中，OA=OC，OB=OD， AC=BD，

∴ OA=AC，OB=BD.

又∵ AB=AC，

∴ OA=OB=AB，

即△OAB是等边三角形；

（2）在Rt△ABC中，AB=1，AC=2，

根据勾股定理，得BC=，

作DE⊥AC于E，

∴ DE·AC=AD·DC，

∴ DE=