题目内容
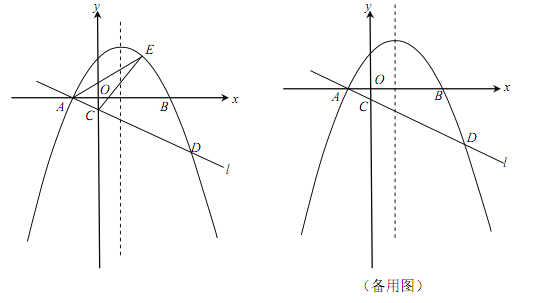
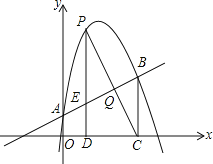
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
【答案】(1)y=-x2+![]() x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(
x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用直线解析式可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(2)设出P点坐标,则可表示出E点坐标,则可表示出PE的长,利用二次函数的性质可求得PE的最大值;
(3)由条件可知四边形BCEP为平行四边形,可得BC=PE,则可求得P点坐标,利用中点坐标可求得Q点坐标.
(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=![]() x+1上,
x+1上,
∴点B的坐标为(4,3),
∴抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴![]() ,解得
,解得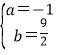 ,
,
∴抛物线的解析式为y=-x2+![]() x+1;
x+1;
(2)设动点P的坐标为(x,-x2+![]() x+1),则点E的坐标为:(x,
x+1),则点E的坐标为:(x,![]() x+1),
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=-x2+![]() x+1-(
x+1-(![]() x+1)=-x2+4x=-(x-2)2+4,
x+1)=-x2+4x=-(x-2)2+4,
∴当x=2时,PE的最大值为4;
(3)∵PC与BE互相平分,
∴四边形BCEP为平行四边形,
∴PE=BC,
∴-x2+4x=3即x2-4x+3=0,解得x1=1,x2=3,
∵点Q分别是PC,BE的中点,且点Q在直线y=![]() x+1
x+1
∴①当x=1时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
②当x=3时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
综上可知点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案