题目内容
 如图,若∠A=∠B=90°,要证明△ADE≌△BED,还需要什么条件?把这些条件写出来,并在括号内填上判定它们全等的理由.
如图,若∠A=∠B=90°,要证明△ADE≌△BED,还需要什么条件?把这些条件写出来,并在括号内填上判定它们全等的理由.(1)
∠AED=∠BDE
∠AED=∠BDE
.(AAS
AAS
)(2)
∠ADE=∠BED
∠ADE=∠BED
.(AAS
AAS
)(3)
AD=BE
AD=BE
.(HL
HL
)(4)
AE=BD
AE=BD
.(HL
HL
)分析:本题除了∠A=∠B=90°,隐含条件为DE=DE(公共边),可选择利用AAS或HL定理证明.
解答:解:(1)添加∠AED=∠BDE,利用AAS可证明△ADE≌△BED;
(2)添加∠ADE=∠BED,利用AAS可证明△ADE≌△BED;
(3)添加AD=BE,利用HL可证明△ADE≌△BED;
(4)添加AE=BD,利用HL可证明△ADE≌△BED;
故答案为:∠AED=∠BDE、AAS;∠ADE=∠BED、AAS;AD=BE、HL;AE=BD、HL.
(2)添加∠ADE=∠BED,利用AAS可证明△ADE≌△BED;
(3)添加AD=BE,利用HL可证明△ADE≌△BED;
(4)添加AE=BD,利用HL可证明△ADE≌△BED;
故答案为:∠AED=∠BDE、AAS;∠ADE=∠BED、AAS;AD=BE、HL;AE=BD、HL.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
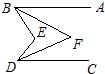 如图,若AB∥CD,∠ABE和∠CDE的平分线交于点F,且∠BED=75°,那么∠BFD等于( )
如图,若AB∥CD,∠ABE和∠CDE的平分线交于点F,且∠BED=75°,那么∠BFD等于( )| A、35° | B、37.5° | C、38.5° | D、36° |
 如图,若大圆半径为R,小圆面积是大圆面积的
如图,若大圆半径为R,小圆面积是大圆面积的
 (1997•重庆)如图.若△ABC的BC边上的高为AH,BC长为30cm,DE∥BC,以DE为直径的半圆与BC切于F,若此半圆的面积是18πcm2,则AH=
(1997•重庆)如图.若△ABC的BC边上的高为AH,BC长为30cm,DE∥BC,以DE为直径的半圆与BC切于F,若此半圆的面积是18πcm2,则AH=